Newsletter
Suscríbete a nuestro Newsletter y entérate de las últimas novedades.
https://centrocompetencia.com/wp-content/themes/Ceco
Los análisis económicos son a menudo un componente clave de la discusión en libre competencia, por lo que es esencial que los abogados que ejercen en el área comprendan los principios económicos básicos y puedan aplicar y transmitir estos conceptos de manera efectiva ante las autoridades de competencia. De lo contrario, se arriesga a perder credibilidad y, eventualmente, perder un caso.
Incluso si un abogado no tiene un conocimiento profundo de las matemáticas y la estadística detrás del análisis experto, al menos debiera aprender y aplicar los conceptos e ideas esenciales para conseguir una mejor comprensión de los análisis cuantitativos, así como de los elementos más vulnerables que amenazan su validez.
En un reciente artículo publicado en la revista The Antitrust Source, de la American Bar Association (Volumen 20, Issue 3), el economista y director asociado del NERA Economic Consulting, Ai Deng, utiliza ejemplos del mundo real para explicar cuatro conceptos económicos clave a una audiencia no experta. Específicamente, el artículo explica (1) qué es un análisis contrafactual, describiendo algunos enfoques comunes, (2) qué es una regresión, (3) la diferencia entre análisis causal y predictivo, ampliamente utilizados en litigios, y (4) el peligro de la “minería de datos” (en inglés, “data mining”) y por qué los abogados deben preocuparse de este riesgo.
El documento comienza relatando una entrevista al actor Keanu Reeves, donde se le preguntó si pensaba que sus años de experiencia como actor lo habían ayudado a convertirse en una mejor persona: “[Es] difícil para mí decir, contrastar y comparar” -respondió el actor-, “porque no tengo nada con que contrastarlo (…) trabajo como actor desde los quince, dieciséis, entonces no sé lo que es no ser [actor]…”. Y es que esta respuesta captura perfectamente el problema fundamental a la hora de encontrar efectos causales de fusiones o en litigios en los niveles de competencia de alguna industria en particular: ¿Cómo podemos saber lo que hubiese pasado si las cosas hubiesen sido diferentes?
Esto último no es otra cosa que preguntarse por el contrafactual. Se trata de un escenario hipotético alternativo que resulta idéntico al escenario existente, salvo por la presencia de aquello que interesa estudiar.
Por ejemplo, si queremos demostrar que los aumentos en precios en un mercado se deben a la conducta de un cartel -y no a otros factores externos-, habría que encontrar un mundo paralelo que sea igual al nuestro, pero cuya única diferencia sea la ausencia de la conducta colusiva. Solo a partir del contraste entre estos dos escenarios es que se podría decir que hay un efecto causal entre la colusión y el alza en precios, de lo contrario no podríamos descartar la existencia de otros factores desconocidos que estarían afectando en los precios.
Claramente, realizar un ejercicio de esa magnitud sólo es posible para la ciencia ficción. Sin embargo, lo que sí es posible hacer -el enfoque comúnmente utilizado por economistas- es construir un contrafactual de manera artificial que sea suficientemente válido como para hacer comparaciones. El autor habla de “benchmarking” para referirse a este escenario, y lo ilustra con un caso práctico de sobreprecio por carteles.
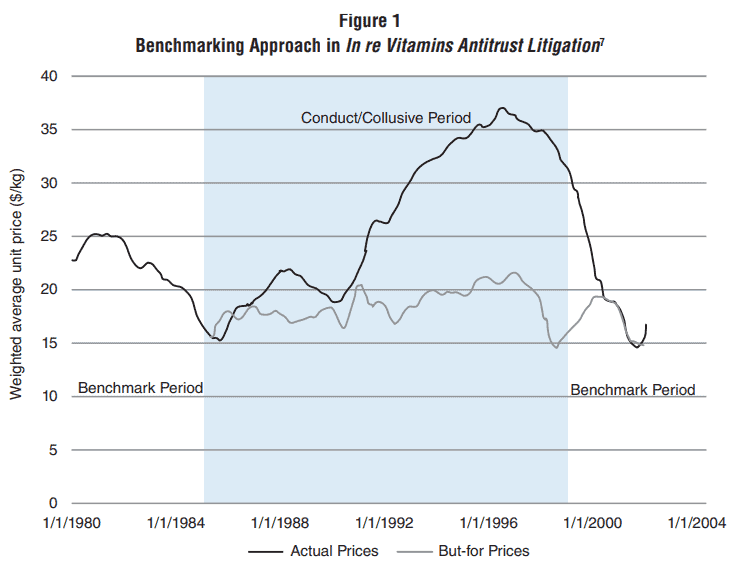
Figura 1: Comparación Antes-Después Precios Medicamentos
La Figura 1 muestra los precios reales del aceite de acetato de vitamina E durante el periodo colusivo, y la evolución de precios en el período anterior al cartel como comparación.
¿Podemos usar el historial de precios como contrafactual válido? Por un lado, al estar usando datos de un mismo mercado, se mantienen constantes varios factores vinculados con su estructura de mercado, barreras de entrada y determinantes del precio de equilibrio. Por otra parte, si cada período se enfrentó a distintas condiciones económicas externas (por ejemplo, si entremedio ocurrió una crisis financiera), entonces el contrafactual pierde un poco de validez.
Otra alternativa que se ha usado en estos casos es considerar una misma industria, en un mismo periodo, pero en dos zonas geográficas distintas donde la conducta anticompetitiva afectó solo a una. Si ambas zonas geográficas son relativamente similares, excepto por la presencia de la conducta, entonces es razonable usarla como contrafactual o “benchmark”.
Con todo, el autor enfatiza que, para que cualquier evaluación comparativa produzca resultados fiables, se deben cumplir varias otras condiciones. Adicionalmente, y debido a la complejidad en esta clase de análisis, a menudo será necesario utilizar herramientas analíticas para estimar los efectos causales relevantes. Una herramienta comúnmente usada entre economistas es la denominada regresión lineal.
En términos modernos, las regresiones son modelos matemáticos que se utilizan para comprender cómo se relacionan las cosas entre sí. Los economistas los utilizan ampliamente en litigios antimonopolio e investigaciones de fusiones.
Las regresiones pueden explicar, por ejemplo, la relación que podría existir entre la conducta de un cartel y los niveles de precios, o la relación entre el grado de competencia post-fusión y los precios. Si una disminución en la cantidad de firmas compitiendo en el mercado va acompañada de un aumento de precios, decimos que la relación es negativa. Las regresiones lineales de alguna manera buscan encontrar esas relaciones.
¿Cómo operan las regresiones en la práctica? La regresión lineal más simple involucra solo dos variables, que denominaremos X e Y . Por ejemplo, la variable Y puede ser el precio de un producto y X puede ser la cantidad vendida. Una regresión lineal está expresada de la siguiente forma:
Y=c+b*X+e
La variable de interés, Y , a veces se denomina «variable dependiente», «variable de resultado»; la variable X a veces se le llama “variable independiente» o «variable explicativa”. Las constantes c y b se le denominan «coeficientes», aunque la constante c también se conoce como «intercepto”. El parámetro más relevante es el coeficiente b , ya que refleja una relación matemática entre X e Y que, cuando se traza en un gráfico, generará una línea recta. La Figura 2 muestra esta representación gráfica.
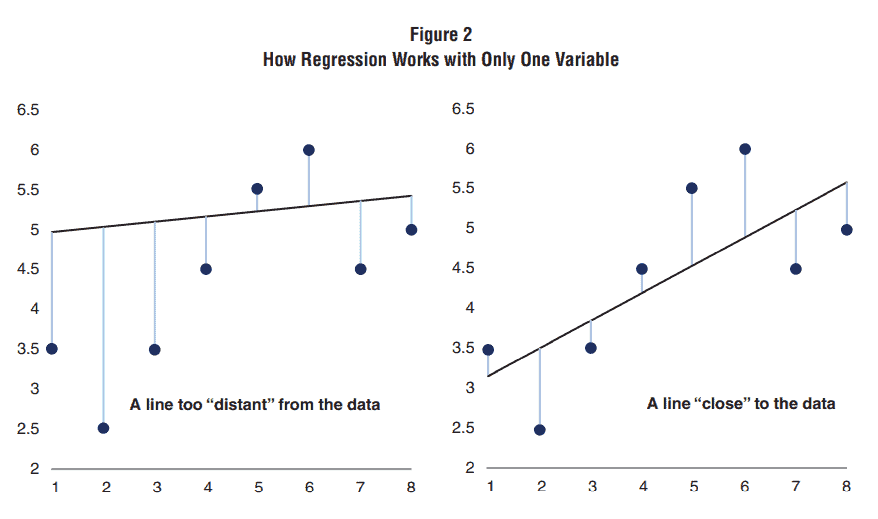
Figura 2: Cómo Funcionan las Regresiones de una sola variable
En la Figura 2, tenemos que ambas líneas son distintas, pese a que sean los mismos datos o puntos. Es más, el segundo gráfico parece estar más cercano en promedio a los puntos. ¿Qué línea representa mejor los datos disponibles? La regresión lineal simple se basa en el método de mínimos cuadrados ordinarios (MCO) que, en esencia, nos dice que la mejor línea se construye a partir de minimizar la diferencia o distancia entre los datos y la línea recta.
Otro término importante que los economistas utilizan a menudo es el coeficiente de determinación o R-cuadrado. En la Figura 2, cuanto más cerca está la línea de todos los datos en promedio, mejor es el ajuste de la regresión, es decir, representa mejor la dispersión de datos. En nuestro ejemplo, la regresión en el panel derecho tiene un mejor ajuste que el 1 en el panel izquierdo. Los economistas usan el R-cuadrado para medir qué tan bien se ajusta una regresión a los datos. Cuanto mayor sea el R2, mejor será el ajuste de regresión. El modelo de regresión en el panel de la derecha tiene un R2 más alto que el de la izquierda.
Finalmente, el término misterioso e también tiene muchos nombres: «término de error» o «perturbación». Para nuestros propósitos aquí, basta pensar en él como un «residuo», que no incluimos porque no podemos observar, pero que también explican cualesquiera que sean las diferencias entre el modelo c+bX .
El autor luego enfoca su atención en la distinción explicar y predecir. ¿Por qué molestarse en hacer esta distinción? Ambos tipos de análisis aparecen en los litigios antimonopolio y cada uno tiene desafíos metodológicos diferentes. No reconocer esta distinción podría conducir a resultados empíricos inferiores y engañosos.
Comencemos con un modelo explicativo, que es cuando queremos medir directamente el efecto de una variable dada sobre otra. Retomando el caso del cartel y su efecto en precios, podríamos estimar la siguiente regresión:
Precio=c+b*Cartel+e
Donde la variable Cartel toma el valor 1 si estamos parados durante el periodo del cartel y 0 si no. En este caso, el valor del coeficiente b nos dirá la diferencia de precios promedio entre estos dos períodos. La Figura 4 ilustra gráficamente la regresión, donde las dos barras horizontales representan los precios promedio durante los períodos sin cartel y sin cartel.
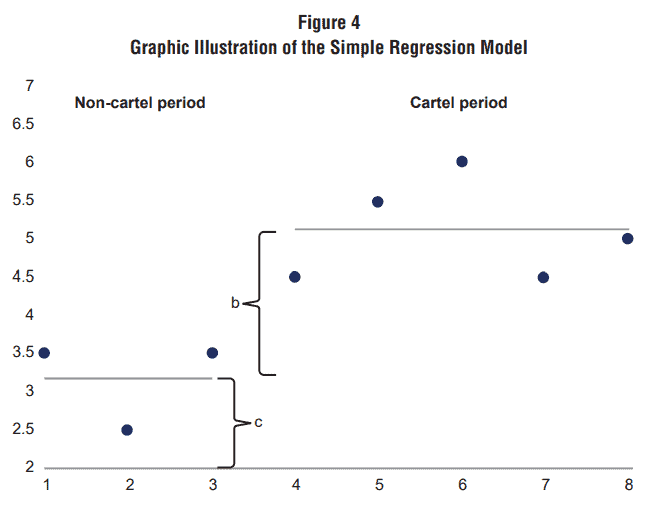
Figura 4: Ilustración Gráfica de un Modelo de Regresión Lineal
Como ya advertimos al inicio, esta estimación tiene el problema de no tomar en cuenta otras variables que también podrían estar afectando la diferencia de precios entre estos dos escenarios. Supongamos que, por ejemplo, hubo algunas interrupciones de suministro nunca antes vistos durante el periodo del cartel debido a desastres naturales. No es necesario entender econometría para reconocer que la diferencia de precios descrita podría estar ignorando el hecho de que una disminución en la oferta también conduce a precios más altos, por lo que la regresión estaría sobreestimando el efecto del cartel.
Casos reales en el ámbito de la libre competencia que hayan aplicado estas herramientas hay varios. Cabe destacar la colusión del Caso Pollos, donde se cuantificó económicamente el daño al consumidor causados por la colusión con el objetivo de aplicar indemnizaciones de perjuicios. Buena parte del desafío empírico consistió en estimar cuánto del sobreprecio ocurrido a nivel de mayorista -producto de la colusión- se traspasó a los precios pagados por los consumidores finales (pass-through). Una primera solución sería estimar la siguiente regresión lineal:
Precio.consumidor=\alpha+\beta_{1}*Precio.mayorista+\beta_{2}*Controles+\varepsilon
Donde el coeficiente \beta_{1} nos diría cuánto cambia el precio minorista ante un cambio en los precios mayoristas. Sin embargo, como ya advertimos, esta regresión podría estar sesgada, ya que existirían factores no observables, tales como shocks de demanda específicos para el consumo de pollo, que no pueden ser controlados en el modelo. Debido a esto, se optó por complementar la regresión con el método denominado variables instrumentales.
Otro ejemplo que ya analizamos en una nota anterior es el cálculo de indemnizaciones por colusión del Caso Farmacias, donde se estimó una regresión lineal (con variables instrumentales) para estimar la elasticidad de la demanda, esto es, qué tan sensible es la cantidad que los consumidores desean adquirir ante cambios en los precios del producto. Este dato es importante para el cálculo del daño por concepto de lucro cesante), consistente en el perjuicio experimentado por los consumidores que no pudieron comprar el medicamento debido al sobreprecio producto de la colusión (para más detalle sobre el concepto, ver Nota CeCo aquí).
Las predicciones juegan un rol importante en el análisis de operaciones de concentración, donde lo que se quiere es predecir el efecto que podría llegar a tener una fusión en variables como el precio. En Chile, un caso reciente fue el análisis de la operación de concentración entre una estación de servicio que funcionaba como independiente y Copec, en la comuna de Hualpén, Región del Bío Bío (para un análisis de esta operación, ver nota CeCo aquí), donde la División de Fusiones de la Fiscalía Nacional Económica (FNE) realizó una serie de regresiones para estudiar el efecto en los precios que tiene la presencia (o salida) de un competidor de bandera blanca adicional “a objeto de aproximarnos al efecto que tendría la materialización de la Operación”. Los resultados del Anexo Económico muestran cómo en la mayoría de los casos existe un efecto negativo y significativo asociado a la presencia de estaciones de bandera blanca (aquellas que no pertenecen a las cadenas tradicionales).
Ahora, cuando el objetivo de un análisis empírico es obtener la mejor predicción posible, debemos adoptar un enfoque diferente. La Figura 5 muestra una serie de tiempo, que podría ser cualquier cosa -por ejemplo, el precio de cierto producto nacional- donde lo que se quiere es predecir los precios del área sombreada a partir de tres modelos de regresión ¿Qué modelo generará predicciones más precisas? El Modelo 1 -una línea recta- captura la tendencia al alza en los datos, pero no captura ninguno de los altibajos reales que se observaron en los datos históricos. El modelo 3, por el contrario, parece capturar la mayoría de los movimientos en los datos históricos.
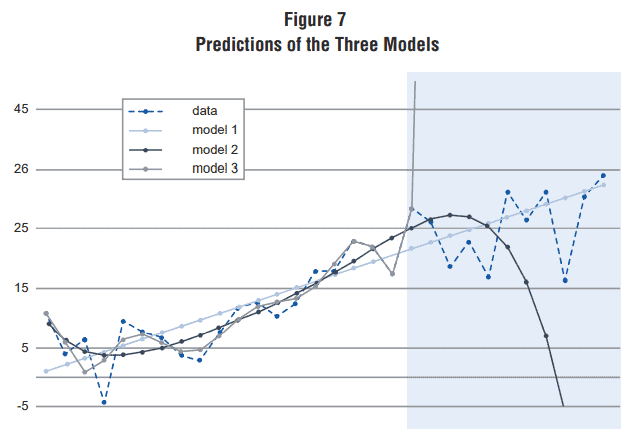
Figura 5: Predicción de tres modelos distintos
¿Por qué entonces el modelo 1 parece ser aquel con mejor capacidad predictiva? ¿Por qué un modelo que se ajusta muy bien a los datos puede predecir tan poco? La intuición dada por el autor es la siguiente: como en el futuro cercano se tiene menos incógnitas, es posible «permitirse» que la regresión se ajuste más estrechamente a los datos históricos; por otro lado, cuanto más tiempo en el futuro queremos predecir, mayor será el número de incógnitas e incertidumbre, lo que requiere un ajuste más flexible para dejar espacio para que se desarrollen. El modelo 1 no se ajusta a los datos históricos tan bien como el modelo 2 o el modelo 3, pero tiene el mejor rendimiento en promedio.
La lección de esto, según el autor, es inmediata: sea escéptico si alguien intenta convencerlo de que su modelo de regresión puede generar una predicción confiable solo porque el modelo se ajusta bien a los datos históricos. Un alto coeficiente de determinación (R-cuadrado) por sí solo no basta como justificación de una predicción.
El autor finaliza advirtiendo sobre el uso del “data mining” como forma de seleccionar minuciosamente aquella información que apoya las preferencias del cliente o del abogado. Según el autor, esto se ha usado en casos recientes como base para excluir informes y testimonios de expertos. En el litigio antimonopolio Processed Egg Products, el experto de los demandantes utilizó un modelo de regresión para relacionar los precios con otros factores. Los demandados pidieron al tribunal que ignorara el modelo de regresión de los demandantes porque si el modelo se estima usando solo un subconjunto de los datos, específicamente usando «solo una determinada transacción del demandado», algunos aspectos de los resultados de la regresión cambian. Los demandantes respondieron que los resultados de los acusados son el producto de una minería de datos inapropiada.
En otro caso de certificación de clase antimonopolio, Pool Products Distribution Market Antitrust Litigation, los demandantes presentaron una moción para excluir el testimonio del experto de los demandados, debido a un supuesto sesgo de extracción de datos que hacía que el testimonio no fuera confiable. El experto de los demandados habría estimado el modelo de regresión utilizando subconjuntos de datos. Sin embargo, el tribunal concluyó que el análisis de sensibilidad de los acusados era «suficientemente confiable» y finalmente rechazó la moción para excluir el testimonio.
Estos casos han mostrado la creciente relevancia de entender los conceptos y herramientas que la estadística y econometría proveen para los análisis de libre competencia. Para el autor, no apreciar estos conceptos claves fácilmente podría resultar en análisis profundamente erróneos y engañosos. El desafío de los abogados está a su vez en comunicar de forma clara y precisa el trabajo de los expertos y, al mismo tiempo, hacer que el análisis del experto sea más sólido.