Newsletter
Suscríbete a nuestro Newsletter y entérate de las últimas novedades.
https://centrocompetencia.com/wp-content/themes/Ceco
volver
En términos generales, la elasticidad es un concepto que cuantifica la medida en que una variable responde a cambios en otra variable. En economía, la elasticidad ( \epsilon ) se utiliza principalmente para medir qué tanto reaccionan los compradores y los vendedores a cambios en las condiciones del mercado (Mankiw, 1997).
La fórmula genérica para calcular elasticidades de la demanda u oferta respecto al precio es:
\epsilon = \frac{\Delta \% Q}{\Delta \% P}
Donde “ \Delta \% Q ” representa el cambio porcentual en la cantidad (demandada u ofertada, dependiendo del tipo de elasticidad que se pretende calcular); y “ \Delta \% P ” representa el cambio porcentual en el precio. Así, la elasticidad mide la sensibilidad de la cantidad demandada u ofertada de un bien respecto al cambio en alguno de sus determinantes, por ejemplo, el precio. Sin embargo, la unidad de análisis que se utiliza en el denominador puede variar si se busca medir la sensibilidad respecto a otra característica (p. ej., el ingreso del consumidor).
Dado que el cambio porcentual de una variable es independiente de las unidades en que se mida dicha variable, la elasticidad es una medida carente de unidades. Esta propiedad facilita la interpretación de la elasticidad y permite su comparación entre diferentes bienes o variables.
La elasticidad precio de la demanda ( {\epsilon}_{P,d} ) mide la sensibilidad de la cantidad demandada de un bien respecto al cambio en su precio, cuando todas las demás variables que influyen en las decisiones de compra de los consumidores permanecen sin cambio —ceteris paribus— (Parkin, 1990).
En concreto, la elasticidad precio de la demanda se calcula mediante la siguiente fórmula:
{\epsilon}_{P,d} = \frac{\Delta \% Q_{d}}{\Delta \% P}
Donde “ \Delta \% Q_{d} ” representa el cambio porcentual en la cantidad demandada.
Considerando que, generalmente, existe una relación inversamente proporcional entre la demanda de un bien y su precio —es decir, un cambio positivo en el precio del bien genera un cambio negativo en la cantidad demandada, y viceversa—, la elasticidad precio de la demanda, generalmente, es negativa.
No obstante, en la práctica, este tipo de elasticidad suele reportarse en valor absoluto; es decir, ignorando el signo negativo. Esto permite enfocarse en su magnitud.
La interpretación de la elasticidad depende del valor numérico obtenido. Por ejemplo, una elasticidad precio de la demanda igual a 2 indica que el cambio experimentado por la cantidad demandada es proporcionalmente dos veces más grande que el cambio del precio. En cambio, un valor de 0,5 indica que el cambio en la cantidad es equivalente, proporcionalmente, a la mitad del cambio en el precio.
De esta forma, se habla de “demanda elástica” si el resultado es mayor que 1; y una “demanda inelástica” si es menor que 1. Por su parte, si el resultado es exactamente 1 —la relación entre demanda y precio es exactamente proporcional—, se habla de “elasticidad unitaria”. En el Gráfico N°1 se pueden observar distintos valores de elasticidad a lo largo de una curva de demanda en forma de línea recta. Estos conceptos serán tratados con mayor profundidad en la sección 4 sobre “Curvas elásticas e inelásticas”.
Gráfico N°1: Elasticidad a lo largo de una curva de demanda
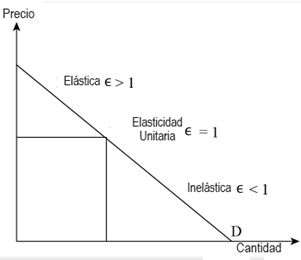
Fuente: Adaptado de homework.study.com
De un modo similar, la elasticidad precio de la oferta ( {\epsilon}_{P,o} ) mide la sensibilidad de la cantidad ofertada de un bien respecto al cambio en su precio, cuando todos los demás factores que influyen en las decisiones de venta permanecen sin cambio (Parkin, 1990).
La elasticidad precio de la oferta se calcula mediante la siguiente fórmula:
{\epsilon}_{P,o} = \frac{\Delta \% Q_{o}}{\Delta \% P}
Donde “ \Delta \% Q_{o} ” representa el cambio porcentual en la cantidad ofertada.
Considerando que la cantidad ofertada de un bien está relacionada, generalmente, de forma positiva con su precio, la elasticidad precio de la oferta es positiva.
La elasticidad precio cruzada de la demanda o, simplemente, elasticidad cruzada de la demanda, mide la sensibilidad de la cantidad demandada de un bien respecto al cambio en el precio de otro bien, cuando el resto de los factores permanece inalterado (Mankiw, 1997).
La elasticidad cruzada de la demanda se calcula mediante la siguiente fórmula:
{\epsilon}_{P,c} = \frac{\Delta \% Q_{d1}}{\Delta \% P_{2}}
Donde “ \Delta \% Q_{d1} ” representa el cambio porcentual en la cantidad demandada del bien 1; y “ \Delta \% P_{2} ” representa el cambio porcentual en el precio del bien 2.
Diferenciándose de la elasticidad “común” de la demanda (respecto al precio propio), que se calcula con valor absoluto, la elasticidad cruzada de la demanda puede ser positiva o negativa dependiendo de la relación que exista entre los dos bienes que se estén analizando (i.e. bienes sustitutos o bienes complementarios).
En particular, dos bienes son sustitutos cuando el incremento en el precio de uno lleva a un incremento en la demanda del otro (en este caso, hay un signo positivo en la elasticidad cruzada de la demanda). Intuitivamente, esto sucede porque los bienes sustitutos satisfacen necesidades similares (p. ej., té y café). Entonces, si el precio del café (bien 2) aumenta, los consumidores preferirán consumir más té (bien 1) que café, y la cantidad demandada por té aumentará. En conclusión, con bienes sustitutos la elasticidad cruzada de la demanda es positiva: un incremento en el precio del bien 2 genera un aumento en la cantidad demandada del bien 1.
En cambio, dos bienes son complementarios cuando el incremento en el precio de uno lleva a una caída en la demanda del otro. Generalmente, esto ocurre porque los bienes complementarios son utilizados en conjunto (p. ej., café y azúcar). El aumento del precio del café puede llevar a que las personas opten por consumir menos de este bien. Así, la cantidad demandada del complemento del café (azúcar) caerá. En este caso, la elasticidad cruzada de la demanda es negativa: un aumento en el precio del bien 2 genera una reducción de la cantidad demandada del bien 1.
La elasticidad ingreso de la demanda ( {\epsilon}_{I,d} ) mide la sensibilidad de la cantidad demandada de un bien respecto a un cambio en el ingreso del consumidor, cuando el resto de los factores permanece inalterado (Mankiw, 1997).
La elasticidad ingreso de la demanda se calcula mediante la siguiente fórmula:
{\epsilon}_{I,d} = \frac{\Delta \% Q_{d}}{\Delta \% I}
Donde “ \Delta \% I ” representa el cambio porcentual en el ingreso del consumidor.
Según el sentido (signo positivo o negativo) de la elasticidad ingreso de la demanda, los bienes pueden ser: bienes normales o bienes inferiores.
En el caso de los bienes normales, la elasticidad ingreso de la demanda es positiva. De manera intuitiva, si el ingreso del consumidor aumenta, la cantidad demandada de los bienes normales también aumenta, y viceversa (cuando el ingreso de una persona disminuye, se reducirá la demanda por ese bien). Es necesario mencionar que la mayoría de los bienes tienen un comportamiento “normal”, incluyendo bienes de lujo y de primera necesidad (comida o ropa)
Por otro lado, los bienes inferiores presentan una elasticidad ingreso de la demanda negativa: en la medida que el ingreso del consumidor aumenta, la cantidad demandada de bienes inferiores tiende a disminuir, y viceversa. La comida rápida de bajo costo y el vestuario de mala calidad son ejemplos de bienes inferiores.
Para ejemplificar estos conceptos, supongamos que deseamos calcular la elasticidad precio de la demanda para un bien, del cual disponemos la siguiente información:
Gráfico 2: Curva de demanda
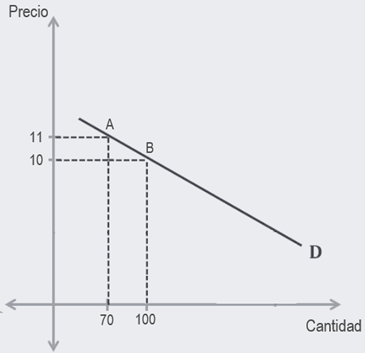
Fuente: Elaboración Propia
Para calcular la elasticidad entre ambos puntos, es necesario obtener los cambios porcentuales del precio y la cantidad demandada.
Genéricamente, el cambio porcentual entre dos puntos se calcula dividiendo la variación por el valor inicial, esto es: \frac{Y_{2}-Y_{1}}{Y_{1}} \times 100 . Aplicando esto a la fórmula de elasticidad precio de la demanda:
{\epsilon}_{P,d} = \frac{(\frac{Q_{2}-Q_{1}}{Q_{1}}) \times 100}{(\frac{P_{2}-P_{1}}{P_{1}}) \times 100}
Donde Q representa la cantidad, P el precio y los subíndices “1” y “2” hacen referencia al punto inicial y final, respectivamente.
Si se considera como punto de partida el punto A, la cantidad y el precio experimentan un cambio porcentual de -30% y 10%, respectivamente:
\Delta \% Q_{d} = (\frac{70-100}{100}) \times 100 = -30\%
\Delta \% P = (\frac{11-10}{10}) \times 100 = 10\%
Entonces, la elasticidad precio de la demanda es:
{\epsilon}_{P,d} = \frac{-30 \%}{10 \%} = |-3| = 3
Sin embargo, si calculamos la elasticidad en el sentido opuesto, tomando como punto de partida el punto B, obtenemos un resultado diferente:
\Delta \% Q_{d} = (\frac{100-70}{70}) \times 100 \approx 43\%
\Delta \% P = (\frac{10-11}{11}) \times 100 \approx -9\%
{\epsilon}_{P,d} = \frac{43 \%}{-9 \%} \approx |-4,7| = 4,7
La diferencia entre ambos resultados es provocada porque los cambios porcentuales son calculados con una base distinta (el respectivo valor inicial).
Una forma de eliminar esta inconsistencia es calcular los cambios porcentuales utilizando como base el “punto medio” entre el valor inicial y final. Esto es:
{\epsilon}_{P,d} = \frac{(\frac{Q_{2}-Q_{1}}{(Q_{1}+Q_{2})/2}) \times 100}{(\frac{P_{2}-P_{1}}{(P_{1}+P_{2})/2}) \times 100}
Con esta metodología, el valor de la elasticidad es el mismo en ambas direcciones:
{\epsilon}_{P,d} = \frac{\frac{100-70}{(100+70)/2}}{\frac{10-11}{(10+11)/2}} = \frac{\frac{70-100}{(100+70)/2}}{\frac{11-10}{(10+11)/2}} \approx |-3,7| = 3,7
Por este motivo, el método del punto medio se considera una medida más precisa de la elasticidad entre dos puntos (Parkin, 1990).
El procedimiento para calcular otros tipos de elasticidades ( {\epsilon}_{P,o} , {\epsilon}_{I,d} , {\epsilon}_{P,c} ) es análogo, pues solo cambian las variables analizadas. Por ejemplo, la fórmula para calcular la elasticidad ingreso de la demanda mediante el método del punto medio es:
{\epsilon}_{I,d} = \frac{(\frac{Q_{2}-Q_{1}}{(Q_{1}+Q_{2})/2}) \times 100}{(\frac{I_{2}-I_{1}}{(I_{1}+I_{2})/2}) \times 100}
Donde I representa el ingreso del consumidor.
Las curvas de oferta y demanda pueden ser clasificadas en función de su elasticidad respecto al precio.
Se dice que la demanda u oferta de un bien es elástica cuando la elasticidad es mayor a 1 ( \epsilon >|1| ); es decir, cuando responde más que proporcionalmente al cambio en el precio. En el caso extremo, cuando la elasticidad es infinita, se dice que la cantidad demandada u ofertada por un bien es perfectamente elástica.
El Gráfico N°3 ilustra una curva de demanda elástica: un pequeño cambio en el precio genera grandes variaciones en la cantidad demandada.
Gráfico N°3: Demanda elástica
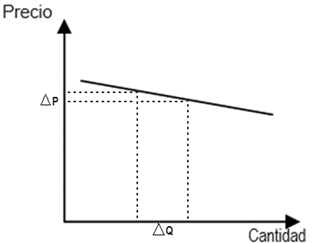
Fuente: Elaboración Propia
El Gráfico N°4 ilustra una curva de demanda perfectamente elástica. En este contexto, la curva de demanda se gráfica como una línea horizontal que cruza al eje ‘Y’ en un solo punto, \bar{P} . Para cualquier precio superior a \bar{P} , la cantidad demandada es cero. Cuando el precio es exactamente \bar{P} , el consumidor está dispuesto a adquirir cualquier cantidad del bien. Cuando el precio es inferior a \bar{P} , la cantidad demandada es infinita.
Gráfico N°4: Curva de demanda perfectamente elástica
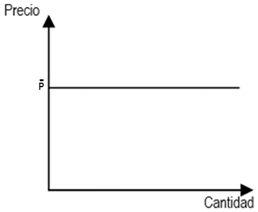
Fuente: Elaboración Propia
Por el contrario, la oferta o demanda de un bien se considera inelástica cuando la elasticidad es menor que 1 ( \epsilon <|1| ), lo que implica que la cantidad se mueve proporcionalmente menos que el precio. Cuando la elasticidad es igual a cero, entonces la curva de oferta o demanda es perfectamente inelástica.
El Gráfico N°5 ilustra una curva de demanda inelástica: grandes variaciones en el precio modifican en muy poco la cantidad demandada.
Gráfico N°5: Demanda inelástica
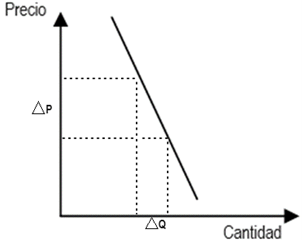
Fuente: Elaboración Propia
El Gráfico N°6 ilustra una curva de demanda perfectamente inelástica. En este escenario, la cantidad demandada está fija ( \bar{Q} ), esto implica que, a cualquier precio, siempre se demanda la misma cantidad del bien. Por ejemplo, los medicamentos esenciales suelen tener una demanda perfectamente inelástica o “muy inelástica”, ya que las personas están dispuestas a pagar cualquier precio por una cantidad fija del medicamento (y cuando están patentados, suelen carecer de sustitutos).
Gráfico N°6: Demanda perfectamente inelástica
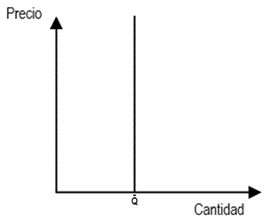
Fuente: Elaboración Propia
Finalmente, cuando la elasticidad es exactamente 1 ( \epsilon =|1| ), la cantidad cambia proporcionalmente igual que el precio y se dice que tiene elasticidad unitaria.
El Gráfico N°7 ilustra una curva de demanda con elasticidad unitaria:
Gráfico N°7: Demanda de elasticidad unitaria
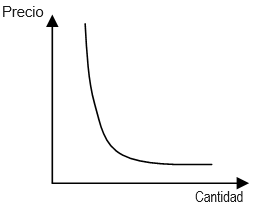
Fuente: Elaboración Propia
Los bienes varían significativamente en sus elasticidades. ¿Qué factores explican que la demanda u oferta de un bien sea más elástica que la de otros?
Disponibilidad de sustitutos
Mientras más o mejores sustitutos existan de un bien, mayor será su elasticidad precio de la demanda, pues los consumidores pueden cambiar fácilmente a otras opciones si el precio aumenta.
Bienes de lujo vs bienes de primera necesidad
Los bienes de lujo suelen ser más elásticos que los bienes de primera necesidad. En concreto, los lujos no son esenciales para la vida cotidiana, por lo que pueden descartarse fácilmente ante un aumento de precios. En cambio, los bienes de primera necesidad (p. ej., alimentos básicos) son difíciles de reemplazar, aun si aumentan sus precios considerablemente.
Proporción del ingreso gastado en el bien
Mientras mayor sea la proporción del ingreso que se gasta en un bien, mayor será su elasticidad precio de la demanda. Los consumidores son más sensibles respecto a la demanda de estos bienes porque una pequeña variación en su precio puede afectar enormemente sus gastos totales.
Horizonte temporal
La elasticidad precio de la demanda de un bien será mayor mientras más tiempo transcurra desde el cambio en el precio. Un mayor horizonte temporal permite a los compradores adaptar sus hábitos de consumo y ajustarse a las nuevas condiciones del mercado.
Naturaleza de la producción
Mientras más sencillo sea adquirir los insumos necesarios para producir un bien, mayor será la elasticidad precio de la oferta. En este sentido, la disponibilidad de insumos facilita que los productores aumenten la cantidad ofertada de un bien ante un aumento del precio. La disponibilidad de capacidad ociosa y la flexibilidad de la tecnología de producción también mejoran la posibilidad de respuesta de los productores.
Horizonte temporal
Del mismo modo que en el caso de la elasticidad precio de la demanda, la elasticidad precio de la oferta de un bien será mayor mientras más tiempo transcurra desde el cambio en el precio. Esto ocurre porque, mientras las posibilidades de producción suelen ser rígidas en el corto plazo, un horizonte temporal suficientemente amplio permite que las empresas pueden reorganizar su producción para ajustarse adecuadamente a las nuevas condiciones del mercado.
La elasticidad es frecuentemente empleada en el análisis económico de casos de libre competencia. Esta herramienta aporta información valiosa para definir mercados relevantes, identificar competidores, evaluar poder de mercado e inferir intensidad competitiva, entre otras aplicaciones.
A continuación, revisamos dos casos ocurridos en Chile en los que se aplicó el concepto de elasticidad.
El 2 septiembre de 2011, Quiñenco se comprometió a adquirir, a través de su filial Enex, la totalidad de los activos tangibles e intangibles de Terpel Chile. Ambas empresas participaban en la distribución y comercialización de combustibles líquidos.
Con fecha 10 de noviembre de 2011, las partes de la operación de adquisición presentaron una consulta ante el Tribunal de Defensa de la Libre Competencia (TDLC), solicitando que la institución declarase si esta se ajustaba a las normas de libre competencia (contenidas en el Decreto Ley N°211). El TDLC dio inicio al procedimiento no contencioso rol NC 400-11/399-11 (causas acumuladas), que contó con la intervención de la Fiscalía Nacional Económica (FNE), asociaciones gremiales y otros actores de la industria.
Entre los antecedentes recabados para la investigación, Quiñenco presentó un informe económico titulado “Un análisis económico de los efectos competitivos de la compra de Terpel por Enex”, elaborado por los economistas Alexander Galetovic, Ricardo Sanhueza y Fernando Díaz. Con la finalidad de evaluar la intensidad competitiva en el mercado analizado, los autores estimaron la elasticidad precio de la demanda que enfrentaba cada una de las estaciones de servicio operadas por Enex.
El informe consideró que las elasticidades estimadas eran “grandes”: en regiones la mínima elasticidad observada fue de 9,0 y en la Región Metropolitana fue de 11,6. Según estas estimaciones, si alguna estación de servicio de Enex aumentaba ligeramente sus precios, se vería reducida drásticamente la cantidad demandada que enfrentaba. De este modo, los autores interpretaron estos resultados como evidencia de que la intensidad competitiva era alta, afirmando que en estas condiciones las firmas no podían ejercer poder de mercado. En línea con lo anterior, los economistas concluyeron que la operación analizada no suponía riesgos anticompetitivos.
Sin embargo, el 26 de abril de 2011, el TDLC rechazó la operación, señalando la existencia de riesgos unilaterales y coordinados que no se verían compensados por ninguna de las eficiencias alegadas por las Partes.
Fue así que las Partes solicitaron a la Corte Suprema que enmendara la sentencia, declarando que la operación consultada cumplía con las normas de libre competencia. Con fecha 2 de enero de 2013, la Corte Suprema acogió la reclamación, aprobando la operación sujeta a medidas de mitigación.
En particular, la Corte Suprema declaró que no se podía afirmar que la operación generase una reducción significativa de la competencia, indicando que, si bien el mercado de distribución de combustibles líquidos era uno concentrado y con características oligopólicas, no existía evidencia concreta que indicara que la fusión aumentaría los riesgos de coordinación.
El 30 de noviembre del 2011, la FNE requirió a tres empresas productoras de pollo (Agrosuper, Ariztia y Don Pollo), y a la Asociación de Productores de Pollo (APA), ante el TDLC. Estas entidades fueron acusadas de celebrar un acuerdo colusorio que limitaba la producción de pollo, controlando la cantidad producida y ofertada en el mercado nacional.
Para evaluar los potenciales efectos anticompetitivos del acuerdo, la FNE definió como mercado relevante la “producción, comercialización y distribución mayorista de carne de pollo fresca en todo el territorio nacional”.
Las empresas requeridas alegaron que la carne de otros animales, como cerdo y vacuno, también debía ser considerada como parte del mercado relevante. Para respaldar su postura, estas empresas citaron estudios de elasticidad cruzada entre la carne de pollo y la de cerdo y vacuno. Estos estudios evidenciaron que la elasticidad cruzada de la demanda estaba en un rango entre 0,4-0,5. En efecto, la estimación de elasticidades cruzadas de la demanda respecto a la carne de pollo, al tener signo positivo ( \epsilon >|0| ), exhibían una relación de sustitución entre los distintos tipos de carne.
Sin embargo, el TDLC señaló que el hecho de que dos bienes presenten un patrón de sustitución no es suficiente para afirmar que ambos productos pertenecen al mismo mercado relevante, debiendo considerar otras variables y metodologías en el análisis (Considerando 24°). En concreto, el TDLC consideró distintos elementos de la demanda que podían desmentir la tesis de sustituibilidad sostenida por las empresas avícolas, tales como el interés de los consumidores por adquirir una variedad de productos, la existencia de descuentos en las otras carnes y la posibilidad de congelar las carnes (pudiendo el consumidor distribuir su consumo entre las distintas carnes durante el tiempo).
Finalmente, el TDLC acogió el requerimiento y condenó a las tres empresas y a la APA por colusión en la producción y asignación de cuotas en el mercado de carne de pollo fresca, entre los años 1994 y 2010. La Corte Suprema confirmó la sentencia y aumentó la sanción monetaria para la APA.