Newsletter
Suscríbete a nuestro Newsletter y entérate de las últimas novedades.
https://centrocompetencia.com/wp-content/themes/Ceco
volver
Cuando un sujeto debe tomar una decisión, el resultado que obtenga dependerá no solo de sus propias acciones, sino también de las decisiones que tomen otros individuos que interactúan directa o indirectamente con él.
La teoría de juegos es una rama de las matemáticas que se enfoca en analizar el comportamiento estratégico de los individuos y cómo este puede afectar los resultados de una interacción entre ellos. Es útil para analizar diversas situaciones de interés económico (p. ej., mercados oligopólicos, asimetrías de información, subastas o licitaciones y cumplimiento bajo contratos incompletos). Sin embargo, su aplicación no solo se enmarca en la economía, sino también en ciencia política, psicología, biología e informática, entre otras áreas. Básicamente es utilizada para modelar situaciones de negociación, conflictos, competencia, cooperación y otros tipos de interacciones análogas.
El objetivo final de la teoría de juegos es determinar la mejor estrategia posible para cada jugador y el resultado que se puede esperar en cada situación.
Los primeros desarrollos de esta teoría se encuentran en el trabajo escrito en 1944 por John von Neumann (matemático) y Oskar Morgenstern (economista), que se titula “Theory of Games and Economic Behavior”.
Los “juegos” pueden clasificarse de diferentes maneras. Pueden ser de suma cero, es decir, lo que gana un jugador es exactamente lo que pierde el otro, o de suma no cero, es decir, lo que gana un jugador puede no ser exactamente lo que pierde el otro. También se pueden clasificar en juegos cooperativos, en los que los jugadores trabajan juntos para alcanzar un objetivo común, y juegos no cooperativos, en los que los jugadores están en competencia directa entre sí.
Por otro lado, la clasificación de los juegos también puede darse por la temporalidad de las acciones de los jugadores, distinguiéndose entre juegos estáticos, en donde los jugadores actúan en simultaneo, o juegos dinámicos, en los cuales los jugadores actúan de forma secuencial.
En relación a esta última clasificación, cabe señalar que es fundamental entender el contexto o la situación en que está desenvuelto el “juego”, ya que la interacción estratégica puede manifestarse de distintas formas y dependerá directamente de este contexto. Así, la situación estratégica más sencilla que podemos pensar es una en la cual cada agente involucrado debe tomar una decisión de forma simultánea, considerando el efecto que tienen las decisiones de los demás en el resultado propio. Este es un juego de tipo “estático”, y un ejemplo concreto se observa en el juego “piedra, papel o tijeras”, en donde dos personas actúan de forma simultánea, ambos conocen las posibles estrategias del rival, y el objetivo es escoger una estrategia que sea “superior” y venza a la opción del rival. Los dos jugadores deben mostrar su opción al mismo tiempo, y el juego no se repite (por lo tanto, no hay información u otro turno para utilizar la información del rival).
Una situación algo más compleja se puede ejemplificar en el juego de ajedrez. Cada jugador toma decisiones en función de lo que ha ocurrido previamente y de lo que espera que ocurrirá en el futuro. En este escenario existe un elemento secuencial relevante, pues las decisiones tomadas por un jugador incidirán en las siguientes jugadas. Este es un juego de tipo “dinámico”.
Antes de entrar de lleno a los distintos tipos de juegos, es necesario conocer algunas los elementos que permiten estructurar un juego.
Hay 4 elementos fundamentales para entender la teoría de juegos: (i) los jugadores, (ii) la estrategia, (iii) los pagos, y (iv) las reglas del juego.
Los jugadores son los agentes económicos (individuos, firmas, organizaciones, países, etc.) que toman las decisiones relevantes del juego o la situación a analizar.
En segundo lugar, es necesario tener una estrategia (o una gama de estas). Las estrategias explicitan cuál es la decisión por la que optará cada jugador, y entre cuáles alternativas puede elegir. En un juego sencillo las opciones de estrategia se pueden simplificar a una decisión dicotómica (p. ej., “cooperar” o “no cooperar” en algún acuerdo), mientras que en juegos más complejos la estrategia puede ser un conjunto de acciones que, de forma complementaria, entregan un resultado para el jugador.
Luego están los pagos. Estos corresponden a la valoración (o utilidad esperada) que tienen los individuos respecto de los posibles resultados del juego. Generalmente se asignan de forma numérica, para denotar su carácter ordinal.
Por último, es necesario conocer las reglas del juego. En términos generales, estas reglas definen el timing del juego, es decir, si las decisiones de los jugadores se toman de forma simultanea o secuencial (es decir, con algún elemento de temporalidad). Además, estas reglas determinaran el grado de información (incertidumbre) que tiene cada jugador al momento de realizar su jugada.
Con todo lo anterior, un juego sencillo puede resumirse en la siguiente Tabla:
| Tabla 1: Matriz de Ejemplo | ||
|---|---|---|
| Jugador A/Jugador B | Estrategia 1 | Estrategia 2 |
| Estrategia 1 | a,b | e,f |
| Estrategia 2 | c,d | g,h |
| Fuente: Elaboración Propia | ||
En donde, se observan a dos jugadores (A y B), las posibles estrategias (Estrategia 1 y 2) y los pagos asociados a cada conjunto de estrategias (a-h). En cada par de estrategias, las letras de la izquierda representan el pago para el jugador A, mientras que las letras de la derecha el pago para el jugador B. Por ejemplo, si el jugador A escoge la estrategia 2, y el jugador B la estrategia 1, el pago para A será “c”, mientras que para B será “d”.
El ejemplo más sencillo para explicar los conceptos anteriores es el conocido juego del “dilema del prisionero”. Este es un juego de suma no cero, no cooperativo y estático.
En este juego, dos jugadores son arrestados y puestos en celdas separadas. La policía cuenta solo con pruebas para encarcelar a uno de los delincuentes, pero si uno de los dos coopera y delata a su compañero, tendrá el beneficio de reducir su condena. Los delincuentes, previamente, han acordado mantener silencio y no delatar a su compañero. Cada uno de ellos tiene dos posibles estrategias: (i) confesar y cooperar con la policía, traicionando a su compañero para reducir su pena o (ii) no confesar y mantener el acuerdo de no delatar a su compañero.
Si ambos cooperan, reciben una sentencia reducida. Si ambos traicionan, reciben una sentencia más larga. Si uno coopera y el otro traiciona, el delincuente que traicionó recibe una sentencia muy reducida y el delincuente que cooperó recibe la sentencia más larga (este es el denominado “sucker’s payoff”). Este juego se resume en la Tabla 2.
| Tabla 2: Dilema del prisionero | ||
|---|---|---|
| Jugador A/Jugador B | confesar | no confesar |
| confesar | -2,-2 | 0,-3 |
| no confesar | -3,0 | -1,-1 |
| Fuente: Elaboración Propia | ||
Se puede observar que la matriz presenta a ambos jugadores (A y B), los cuales tienen la posibilidad de escoger entre dos opciones (estrategias): (i) confesar y (ii) no confesar. Cada estrategia tiene un pago asociado (que se representa numéricamente). En este juego, los pagos hacen referencia a los años de condena, es decir -1 corresponde a 1 año de condena.
El número a la izquierda es el pago asociado al jugador A, mientras que el número a la derecha es el pago asociado al jugador B. Por ejemplo, si ambos jugadores escogen “confesar”, los dos reciben dos años de cárcel (-2 de pago). Por otro lado, si el jugador A escoge “no confesar” y el jugador B escoge “confesar”, el jugador A recibe tres años de cárcel (-3 de pago), mientras que el jugador B queda libre (0 de pago). Por último, si ambos “no confiesan” reciben de pago solamente 1 años de cárcel.
El dilema está en el actuar de los jugadores. Si actúan racionalmente, es decir, maximizan su propio beneficio, cada uno preferiría “confesar”, independientemente de lo que haga el otro.
Este resultado se debe a que la decisión del individuo en el juego depende de lo que haga el otro. En un juego de este tipo, en el que los participantes interactúan de manera independiente, la mejor estrategia para cada individuo no es necesariamente la mejor estrategia para el conjunto de participantes. Es decir, la búsqueda individual del interés propio puede llevar a un resultado global subóptimo (que en este caso sería [no confesar, no confesar]).
En este juego, ambas opciones son racionales para cada jugador, pero la mejor opción para ambos jugadores juntos es no confesar, lo que da como resultado una sentencia reducida para ambos. Sin embargo, debido a la posibilidad de traición, los jugadores pueden terminar eligiendo traicionar en lugar de cooperar, lo que da como resultado una sentencia más larga para ambos.
El objetivo de estudiar teoría de juegos es tener herramientas para realizar predicciones sobre cuál es el resultado esperado dada una situación estratégica entre dos o más agentes.
En el ejemplo del dilema del prisionero, cada jugador se pregunta personalmente cuál será el comportamiento del otro jugador. Si pienso que el otro va a confesar, entonces mi mejor respuesta ante la estrategia que tomará el otro jugador es confesar, y así reducir mi condena. Por otro lado, si el jugador no coopera con la policía, mi mejor estrategia es confesar, dado que así no recibo condena (pago 0).
Entonces, la clave está en que, sin importar la estrategia que opte el otro jugador, mi mejor estrategia será “confesar”. En este caso, llamaremos a “confesar”, como una estrategia dominante, es decir, la estrategia que otorga un pago mayor, sin importar cuál es la estrategia que siga el otro.
Dado que el juego del dilema del prisionero es simétrico (es decir, otorga igual pago para ambos jugadores), para cada jugador la estrategia dominante es “confesar”.
Aunque el concepto de estrategia dominante resulta intuitivo y un buen predictor para el potencial resultado de un juego, en la mayoría de las situaciones la estrategia óptima de un jugador dependerá (y variará) según la(s) estrategia(s) que opte el otro jugador.
También existirán casos en donde un juego no presentará estrategias dominantes. Un ejemplo de esto es el dilema del viajero (juego de suma no cero, no cooperativo y dinámico). En esta situación, dos viajeros deben decidir si conducir o tomar el tren para llegar a una conferencia. Si ambos toman el tren, llegan a tiempo y obtienen una puntuación de 3 puntos cada uno. Si ambos conducen, se retrasan con el tráfico y obtienen una puntuación de 1 punto cada uno. Si uno toma el tren y el otro conduce, el que toma el tren llega a tiempo y obtiene una puntuación de 5 puntos, mientras que el que conduce llega tarde y obtiene una puntuación de 0 puntos. La matriz de pago para este juego se presenta en la Tabla 3.
| Tabla 3: Dilema del viajero | ||
|---|---|---|
| Jugador A/Jugador B | Conducir | Tomar el tren |
| Conducir | 1,1 | 0,5 |
| Tomar el tren | 5,0 | 3,3 |
| Fuente: Elaboración propia en base a Modelo de lenguaje ChatGPT (2023). | ||
En este juego, no hay una estrategia dominante para ninguno de los jugadores. Si A conduce, B obtendrá una puntuación más alta si toma el tren. Si A toma el tren, B obtendrá una puntuación más alta si conduce. Lo mismo ocurre para B. Por lo tanto, ambos jugadores tienen que tener en cuenta las decisiones del otro al tomar su propia decisión.
Si los dos jugadores cooperan y toman el tren, obtendrán una puntuación total de 6 puntos (la más alta socialmente). Si ambos compiten y conducen, obtendrán una puntuación total de 2 puntos. Si uno toma el tren y el otro conduce, obtendrán una puntuación total de 5 puntos. Por lo tanto, en este juego, la cooperación es mejor que la competencia para ambos jugadores, pero la solución cooperativa depende de la elección de estrategia del otro jugador.
El equilibrio de Nash se utiliza para analizar la interacción estratégica entre dos o más jugadores. Se basa en la idea de que cada jugador elige las estrategias que maximiza su pago esperado, dada la estrategia elegida por los demás jugadores. Se define como una combinación de estrategias en la que ningún jugador tiene incentivos para cambiar su estrategia, dado que los demás jugadores también mantienen sus estrategias.
John Nash, premio Nobel de Economía en 1994 por sus contribuciones a la teoría de juegos, fue el primero en describir formalmente este concepto en su trabajo «Equilibrium Points in N-person Games«, en 1950. En él, Nash afirma que “el concepto de equilibrio de Nash es el concepto central de la teoría de juegos”.
El equilibrio de Nash se aplica a una amplia variedad de juegos, desde juegos simples (como el dilema del prisionero) hasta juegos más complejos (como los juegos dinámicos). En la teoría de juegos, el análisis de equilibrio de Nash se utiliza para encontrar las estrategias óptimas de los jugadores en diferentes tipos de juegos y predecir cómo evolucionará una interacción estratégica.
Un juego es estático cuando los jugadores actúan de forma simultánea, es decir, no en un sentido cronológico, sino sin saber lo que los otros jugadores han escogido. Es importante mencionar que, aunque un juego sea estático, esto no quiere decir que sea tenga información incompleta. En consecuencia, este tipo de juegos se pueden clasificar entre aquellos en los que existe información completa y en los que existe información incompleta.
Un juego estático con información completa es el dilema del prisionero. Como ya se explicó, en este caso ambos jugadores conocen las posibles estrategias del otro jugador, y sus pagos. Solamente tienen la incertidumbre de cuál será la decisión del otro (ya que deben decidir su estrategia al mismo tiempo).
Por otro lado, un ejemplo de un juego estático con información incompleta son las subastas. En este juego, los jugadores (empresas) compiten para adquirir un objeto (p. ej., la licitación de un proyecto) a través de una subasta. Los jugadores no conocen los valores que los demás jugadores están dispuestos a pagar, es decir, desconocen el valor que los demás jugadores asignan al objeto.
En la subasta, los jugadores hacen ofertas. El jugador que realiza la oferta más alta gana el objeto y paga su oferta. El objetivo de los jugadores es adquirir el objeto al menor costo posible, pero la estrategia que cada jugador utiliza dependerá de su propia valoración del objeto y de su percepción de la valoración de los demás jugadores.
Otro ejemplo de juego estático con información completa son los del tipo “Matching Pennies”. Sin embargo, a diferencia de los ejemplos anteriores, en donde la cooperación era un elemento fundamental, en el siguiente ejemplo se explica un juego de suma cero, en donde el éxito de un jugador depende del fracaso del otro. La matriz de este juego se presenta en la Tabla 4.
| Tabla 4: Matching Pennies | ||
|---|---|---|
| Jugador A/Jugador B | Cara | Sello |
| Cara | 1,-1 | -1,1 |
| Sello | -1,1 | 1,-1 |
| Fuente: Elaboración propia | ||
Cada jugador tiene una moneda y debe mostrar una cara de ésta. Si ambos jugadores muestran la misma cara, entonces el jugador A gana el juego (1 punto), mientras que si muestran distintas caras el jugador B gana el juego (1 punto). En este caso, a cada jugador le gustaría saber qué es lo que haría el otro (y al mismo tiempo, que el otro no conozca lo que él hará).
De una forma similar, pensemos en la ejecución de un penal de futbol, en donde hay dos jugadores (pateador y arquero), que tienen 3 opciones (estrategias) cada uno: (i) izquierda, (ii) centro y (iii) derecha. El éxito de cada uno depende directamente del fracaso del otro.
Por último, un ejemplo de coordinación en un juego estático es el de “batalla de los sexos”, en donde se plantea una cita entre dos jugadores y ellos olvidaron el lugar de encuentro. El mayor pago se recibe cuando ambos escogen el mismo lugar (p. ej., partido de fútbol o museo), pero no tienen la posibilidad de contactarse para coordinarse. Además, cada uno tiene preferencias de un lugar por sobre el otro (es decir, le reporta mayor utilidad). En este caso, el jugador A prefiere ir al partido de fútbol por sobre el museo, y el jugador B prefiere ir al museo por sobre el partido de fútbol. Sin embargo, el peor escenario para ambos es que no puedan encontrarse y fracase la cita. Este ejemplo se resume en la Tabla 5.
| Tabla 5: Batalla de los sexos | ||
|---|---|---|
| Jugador A/Jugador B | Partido de fútbol | Museo |
| Partido de fútbol | 2,1 | 0,0 |
| Museo | 0,0 | 1,2 |
| Fuente: Elaboración propia | ||
Por lo tanto, es posible darse cuenta de que la forma de resolver estos juegos, o los potenciales resultados, dependerá de los distintos incentivos que tenga cada uno, además de las reglas que se plantan en el juego.
A diferencia de lo planteado anteriormente, un juego es dinámico cuando describe una secuencia de eventos o decisiones que se desarrollan a lo largo del tiempo, y en el que las decisiones tomadas en un momento dado pueden afectar el resultado del juego en momentos posteriores.
En estos casos, cada jugador puede tener varias opciones de acción disponibles en cada punto del tiempo, y la elección de cada jugador puede influir en la elección del otro jugador en el futuro. Las decisiones pueden ser tomadas simultáneamente o en secuencia, y la información disponible para cada jugador puede ser completa o incompleta.
Un ejemplo de un juego dinámico con información completa es el juego de ajedrez. En este, los jugadores conocen todas las posiciones y movimientos de las piezas en el tablero. Así, la información completa permite a los jugadores planificar sus movimientos y anticipar los movimientos de su oponente.
En el ajedrez, los jugadores tienen como objetivo capturar al rey del oponente (jaque mate), lo que finaliza el juego (otorgándole la victoria al que captura el rey). Cada jugador tiene una serie de movimientos disponibles en cada turno, y el juego se desarrolla en una secuencia de turnos.
Otro ejemplo concreto, y relevante para el derecho de competencia, es la competencia entre empresas. Es de esperar que el comportamiento de una empresa (p. ej., su estrategia comercial) sea distinta si la decisión por la que opta la realiza de forma simultánea con su competidor o si la realiza luego de observar qué hace la competencia. Del mismo modo, si una empresa sabe que otras firmas observan su decisión antes de actuar, tendrá en cuenta esto al momento de tomar su decisión (como puede ocurrir, por ejemplo, en el modelo “Líder-Seguidores” en un oligopolio).
Con esto en mente, es relevante incorporar al análisis una dimensión temporal. En el siguiente ejemplo podemos observar el comportamiento de dos países (A y B) que se enfrentan en un conflicto.
El primero en jugar es el país A, el que debe tomar la decisión de invadir o no al país B. En caso de invadir, el país B debe escoger entre pelear o rendirse. La Figura 1 diagrama lo escrito anteriormente en un árbol de decisión.
Figura 1: Árbol de decisión
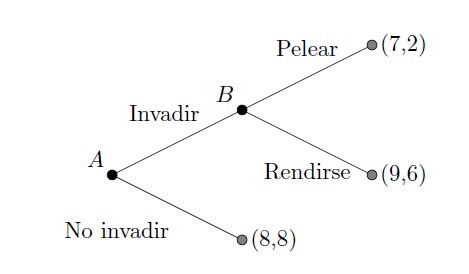
Fuente: Apunte Microeconomía II Teoría de Juegos y Aplicaciones – Gonzalez, Hojman y Sepúlveda (2014)
Esto se conoce como árbol de decisión y permite ilustrar las distintas situaciones que enfrentan los jugadores en juegos dinámicos. Cada círculo negro es un nodo de decisión, y las ramas que surgen de cada nodo son las posibles decisiones que puede tomar cada jugador, en ese nodo. Los círculos grises son nodos terminales, que indican el fin del juego.
Cada nodo de decisión tiene una etiqueta que indica qué jugador toma la decisión. En este caso, el primero en jugar es el país A, y si la decisión es invadir, el país B jugará en el segundo turno. Por último, los nodos terminales tienen asociado un pago (indicado numéricamente entre paréntesis).
En este ejemplo, el mayor pago posible para el país A se logra cuando toma la estrategia de invadir, y el país B decide rendirse, otorgando un pago de 9 y 6, respectivamente. Por su parte, el país B prefiere no ser invadido (recibiendo un pago de 8).
Entonces, ¿qué resultado se puede esperar de este juego dinámico? Para tener una aproximación se puede escribir el juego de forma normal, con una matriz de 2×2, presentada en la Tabla 6.
| Tabla 6: Juego de invasión | ||
|---|---|---|
| País A/País B | Pelear | Rendirse |
| Invadir | 7,2 | 9,6 |
| No invadir | 8,8 | 8,8 |
| Fuente: Elaboración propia en base a González, Hojman y Sepúlveda (2014) | ||
Bajo este formato, existen dos equilibrios de Nash en este juego; [No invadir, Pelear] e [Invadir, Rendirse]. El primero ocurre porque, si el país B está dispuesto a pelear, el país A no tiene incentivos a invadir (su pago será de 7 en vez de 8). Por otro lado, [Invadir, Rendirse] también es un equilibro de Nash porque cuando el país A decide invadir, el país B no tiene incentivos a pelear (su pago será de 6 si se rinde versus 2 si pelea).
Es posible darse cuenta que, en la dimensión dinámica del juego, el equilibrio [No invadir, Pelear] no existe, dado que la estrategia pelear solo se activa si el país A decide invadir.
Por lo tanto, con esto es posible introducir el concepto de equilibro perfecto en subjuegos. En este caso particular, el equilibrio [Invadir, Rendirse], además de ser un equilibro de Nash (donde ningún agente tiene incentivos para desviarse), es un equilibro perfecto en subjuegos, y la explicación está en que es un equilibro que no se basa en una amenaza no creíble.
Para diferenciar un equilibro de Nash de un equilibro perfecto en subjuegos, se utiliza la inducción hacia atrás. Como su nombre lo indica, el juego debe empezar a resolverse desde atrás (nodos terminales) evaluando la respuesta optima y con eso avanzar a los nodos anteriores.
Es posible resolver el ejemplo anterior viendo las posibles decisiones del país B. Entre rendirse (pago de 6) y pelear (pago de 2), el país B decide rendirse. Por otro lado, si el país A decide no invadir, el país B no puede tomar ninguna decisión y recibe un pago de 8.
Luego vamos al nodo de decisión de A, en donde puede optar por invadir o no invadir. El primero le entrega un pago de 9, mientras que no invadir un pago de 8. Por lo tanto, si los países actúan de forma racional, el equilibro perfecto en subjuegos es [Invadir, Rendirse].
La teoría de juegos se aplica en muchos contextos de decisión en materia de competencia. Esto pues, en este ámbito, los diferentes agentes están constantemente inmersos en distintas situaciones y con diferentes incentivos.
En modelos de competencia oligopólica, es común que las empresas actúen de forma estratégica, por lo mismo, es una rama en donde se utiliza de sobremanera la teoría de juegos (ver Investigación de J.L. Bonifaz, “Teoría de Oligopolios y Análisis de Mercado Relevante: El caso del Mercado de Comercialización de Gas Natural Vehicular”).
Siguiendo a González (2011), la colusión puede entenderse como un juego en donde la competencia de las empresas puede reducirse a dos opciones, competir o colaborar entre ellas. Los beneficios asociados a cada estrategia se presentan en la Tabla 7 y dependen tanto de su estrategia como la del rival.
| Tabla 7: Competencia entre empresas | ||
|---|---|---|
| Empresa A/Empresa B | Competir | Colaborar |
| Competir | 20,20 | 50,10 |
| Colaborar | 10,50 | 40,40 |
| Fuente: González (2011) | ||
Si el juego es de una única vez, ambas empresas decidirán competir. Si bien ambas empresas son conscientes de que estarían mejor si colaboran entre ellas, existe el riesgo inherente de que, si una colabora, la otra decida competir capturando las rentas (fijando un precio más bajo) y dejando en peor posición a su rival. Precisamente en este punto radica la inestabilidad de un cartel.
Ahora bien, como sugiere González, la interacción repetida en el tiempo entre las empresas es una forma de sostener una colusión (es decir, la jugada “cooperar”). Si el castigo por desviarse de un acuerdo se puede aplicar en el periodo siguiente (no colaborando nunca más), es posible sostener una colusión en el tiempo.
Como predice la teoría, entre más pacientes sean las empresas, exista un horizonte temporal indefinido (pero de largo plazo) y la posibilidad del castigo sea aplicable en el periodo siguiente de un potencial desvío, un acuerdo colusivo es sostenible en el tiempo.
Considerando este fenómeno, las agencias de competencia implementan distintas herramientas para poder desmantelar estos carteles. La más importante de estas herramientas es la delación compensada. Con ello, las agencias buscan que una empresa se desvié del acuerdo, delatando a su rival y otorgándole inmunidad en el juicio posterior por la práctica anticompetitiva (ver columna de opinión de C. Agostina y F. Irarrázabal “Caso Tissue y los nuevos desafíos para la delación compensada”).
Dependiendo de la jurisdicción, este mecanismo -delación compensada-puede ser aplicado solamente para un agente, o para los dos primeros que delatan, y puede incluir rebajas de pena, eximición total, entre otros beneficios.
De este modo, la teoría de juegos aporta para que las agencias logren crear mecanismos que entreguen los incentivos suficientes para que las empresas opten por la estrategia de desviarse de un acuerdo colusivo y delatar a su rival (ver nota CeCo “La delación compensada y los bajos costos de la colusión en Ecuador”).
Bonífaz, J. L. (2022). Teoría de Oligopolios y Análisis de Mercado Relevante: El caso del Mercado de Comercialización de Gas Natural Vehicular. Investigaciones CeCo.
González, A. (2011). Prácticas colusivas. La libre competencia en el Chile del Bicentenario, 143-160.
Nash Jr, J. F. (1950). Equilibrium points in n-person games. Proceedings of the national academy of sciences, 36(1), 48-49.
Mas-Colell, A., Whinston, M. D., & Green, J. R. (1995). Microeconomic theory (Vol. 1). New York: Oxford university press.
Von Neumann, J., & Morgenstern, O. (2007). Theory of games and economic behavior. In Theory of games and economic behavior. Princeton university press.