Newsletter
Suscríbete a nuestro Newsletter y entérate de las últimas novedades.
https://centrocompetencia.com/wp-content/themes/Ceco


La discusión con respecto al uso de algoritmos para determinar y establecer precios por parte de las empresas, y sus efectos sobre la libre competencia de los mercados, ha estado principalmente enfocada en los posibles efectos coordinados (colusión) que podrían producir (ver Investigación CeCo: “Colusión de IA: ¿Deberíamos estar preocupados?”). En efecto, mejoras en la rapidez para monitorear precios rivales, capacidades computacionales para procesar datos registrados en tiempo real y optimizar decisiones de precios, son factores elementales que pueden facilitar esquemas colusorios (sean explícitos o tácitos). En este sentido, un terreno parcialmente inexplorado en la literatura corresponde a la adopción unilateral de algoritmos y sus efectos en los equilibrios competitivos de los mercados.
En este contexto, en mayo de este año, los autores Zach Brown (Universidad de Michigan) y Alexander Mackay (Universidad de Virginia), publicaron el artículo académico “Algorithmic Coersion with Faster Pricing”. En este, se proponen evaluar cómo una empresa que adopta algoritmos de precios puede coaccionar a sus rivales – de forma unilateral – a subir precios por sobre el equilibrio competitivo. Para ello, los autores desarrollan un modelo empírico de competencia entre dos empresas (una usa el algoritmo y la otra no).
En lo que sigue de esta nota, repasaremos el modelo empleado por los autores, los resultados principales y señalaremos algunas consideraciones adicionales hechas por los autores respecto del diseño de plataformas digitales.
Los algoritmos de precios tienen efectos relevantes sobre las dinámicas del mercado, en la medida que cambian la manera en que las empresas actualizan los precios de sus productos/servicios. Los algoritmos permiten, por un lado, monitorear y reaccionar con mayor rapidez a los precios de la competencia (velocidad de reacción, capturada con el símbolo ‘α’), y por otro, mantener una conducta o estrategia consistente durante varios periodos o “ciclos” (compromiso, capturado con el símbolo ‘γ’). Así, ambas variables (α y γ) son utilizadas por los autores para caracterizar el comportamiento de un algoritmo de precios (ver nota CeCo: “Precios algorítmicos y desafíos de regulación”).
Para aterrizar este comportamiento, el modelo propuesto por los autores contempla dos firmas (A y B) que producen un producto similar. La firma A adopta un algoritmo de precios (con cierto nivel de compromiso temporal) que le permite tener una ventaja de tiempo, mientras que la firma B no lo adopta. Al comienzo de cada periodo, las firmas eligen sus precios, y posteriormente la firma A puede reaccionar con un rezago igual a α. Así, los autores definen el periodo como la frecuencia con la que la firma B (más lenta) actualiza sus precios. Bajo esta lógica, la firma A tendría una ventaja de tiempo equivalente a 1-α, ya que puede establecer sus precios al comienzo del periodo y luego reaccionar con un tiempo de α para actualizar su precio.
Figura 1: Dinámica de timing
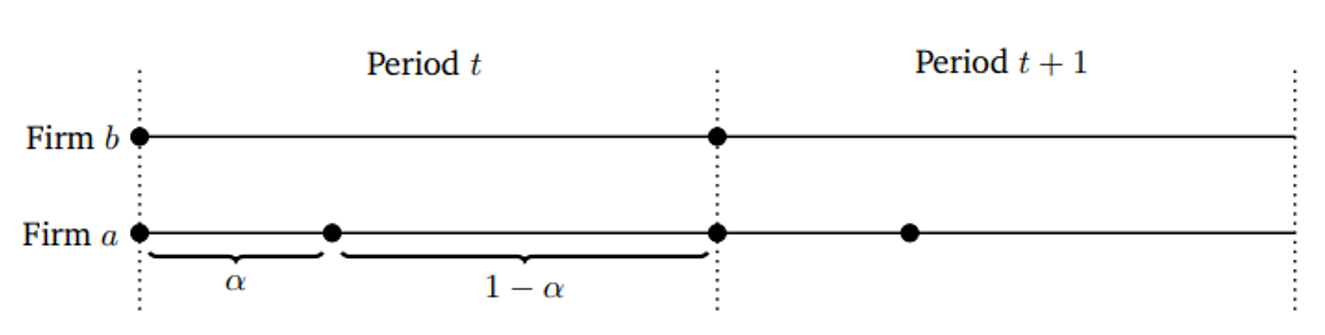
Extraído de Mackay & Brown, 2025, p. 7.
De acuerdo con la Figura 1, la firma algorítmica (A) maximiza su beneficio al comienzo del periodo, y en función de lo observable, puede actualizar su precio según una función de actualización. Al iniciar un nuevo periodo, ambas firmas pueden modificar sus precios, pero la firma B lo hace sin que la firma A tenga información anticipada sobre su decisión. En base a este nuevo precio de la firma B, la firma A vuelve a actualizar su precio, y así sucesivamente. De este modo, en caso de que la firma B, al comienzo de un nuevo ciclo, fije un precio más bajo que el de la firma A, esta última tendrá la oportunidad de castigar —automáticamente— a través de un (potencialmente más bajo) que entra en vigor durante el resto del período. Esta reacción rápida permite a la firma A atraer la demanda residual antes de que B tenga una nueva oportunidad de ajustar su precio.
Como se puede inferir de la figura, cuando α = 0, la firma A tiene máxima rapidez para actualizar sus precios y tiene una ventaja total en términos de velocidad de ajuste. Al contrario, cuando α = 1, ocurre que no tiene ningún tipo de ventaja y se convierte en un juego de precios simultáneos.
Luego de cada periodo, la firma A, con probabilidad γ, permanecerá comprometida a su algoritmo en el siguiente periodo. Esto refleja el hecho de que, en la práctica, una firma reprograma un algoritmo de forma infrecuente (esto es distinto a la capacidad del algoritmo de reaccionar con rapidez). En este sentido, las firmas dejarían actuar al algoritmo durante varios periodos (ciclos), de modo que ‘γ’ captura el grado de compromiso intertemporal de la firma con la estrategia programada, lo que permite que sus amenazas de castigo resulten creíbles para su rival.
El problema de maximización de la firma algorítmica se formula como uno de tipo dinámico, donde la firma decide, por un lado, el tipo de algoritmo al cual se compromete, y por otro, maximiza los beneficios que obtiene mientras permanece sujeta a dicho algoritmo. En contraste, la firma B establece precios únicamente para maximizar beneficios en el periodo o ciclo actual. Si bien esta última (B) conoce la regla de reacción del algoritmo, su comportamiento es miope, por lo que enfrenta cada período como un juego de un solo turno.
Los autores argumentan que este supuesto descarta la posibilidad de equilibrios colusivos estándar, ya que la colusión requiere que las firmas sean forward-looking y consideren los beneficios de mantener estrategias cooperativas en el tiempo. Así, los autores exploran cómo incluso las firmas más ingenuas (naive), que no maximizan sus ganancias considerando el futuro, podría optar por establecer precios más altos por la sola amenaza de castigo por parte de una firma algorítmica.
Considerando lo anterior, los autores evalúan los precios de equilibrio para 4 escenarios, que combinan los valores de α y γ:
Usando una demanda lineal con un elemento de sustitución entre los productos, los autores calculan los equilibrios para cada uno de estos modelos descritos previamente.
Figura 2: Precios de equilibrio para los 4 modelos

Extraído de Mackay y Brown, 2025, p. 12.
Como se puede observar, para el caso donde hay ventaja de precios, pero no hay compromiso (esquina inferior izquierda), los precios para las firmas A y B son un 5% y 14% más altos, respectivamente, que en el equilibrio simultáneo. De forma paralela, cuando hay solo compromiso, pero no ventaja de velocidad, los precios alcanzan niveles similares, pero distribuidos de forma inversa entre las firmas. Ahora bien, el resultado que resulta más interesante es que cuando hay ventaja de precios y compromiso (esquina inferior derecha), los precios son un 93% y un 115% más altos para las firmas a y b. En este sentido, los autores señalan que el punto de referencia colusivo corresponde a la combinación de precios (2,2), por lo tanto, en este escenario, una de las firmas puede alcanzar precios incluso más altos a los del equilibrio colusivo.
Ahora bien, ¿cómo funciona el mecanismo de castigo para llegar a este equilibrio? Cuando la firma B no elige el precio que el algoritmo de la firma A determina como óptimo, la función de actualización de la firma A aplica un castigo, equivalente a la mejor respuesta estática —esto es, la que maximiza sus beneficios en el corto plazo sin cooperar—. Esta respuesta, corresponden a reducir el precio de la firma A de tal forma que disminuye las ganancias de B y desincentiva futuras desviaciones.
Los autores profundizan el análisis contemplando cómo se comportan los equilibrios competitivos al incrementar gradualmente el grado de ventaja de precios y de compromiso de la firma A, tanto en términos de precios como de beneficios.
Figura 3: Precios y beneficios en el equilibrio coercitivo según la ventaja de velocidad
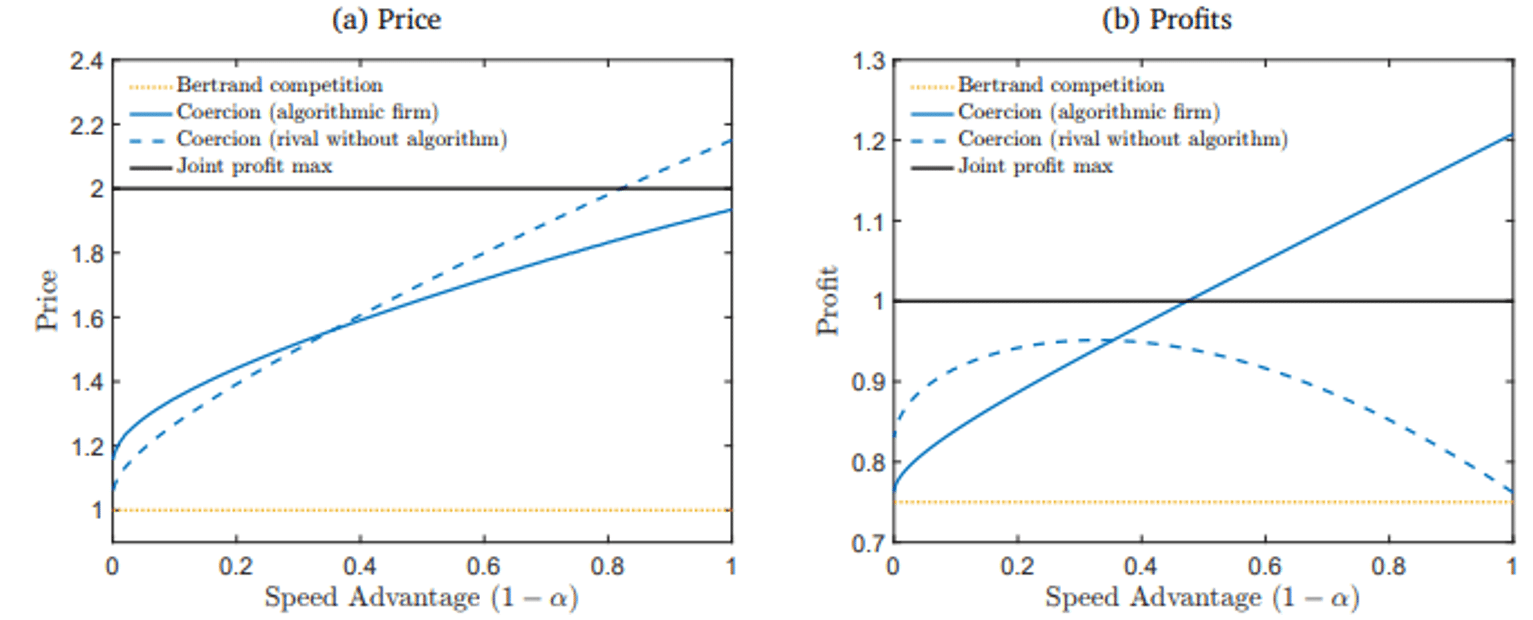
Extraído de Mackay y Brown, 2025, p. 14.
Con respecto al comportamiento del equilibrio dependiendo de velocidad de respuesta, tenemos que el precio para algunos productos puede ser incluso más alto que en el escenario colusivo. De la misma forma, una firma es capaz de extraer rentas sobre-colusivas cuando la rapidez es superior al 50% del periodo (α > 0,5). Cuando la reacción es rápida, entonces ocurre que la firma B no obtiene tantos beneficios al desviarse de los precios colusivos, ya que la firma algorítmica puede castigar con rapidez y redirigir la demanda hacia ella. En este sentido, el equilibrio se mantiene porque el incentivo de la firma B es quedarse en este estado, ya que sus beneficios nunca son menores que aquellos del equilibrio simple y simultáneo. Por el contrario, cuando la ventaja de precios es baja, lo óptimo para la firma algorítmica es liderar con un precio más alto que el rival, utilizando la amenaza de castigo para evitar que la firma B baje el precio aún más.
En un ejercicio alternativo, los autores revisaron el cambio de precios y beneficios ante cambios en el nivel de compromiso (considerando un máximo nivel de ventaja de tiempo). En este caso, la firma algorítmica siempre establece precios más bajos y obtiene beneficios más altos. Por su parte, el rival siempre obtiene beneficios muy similares a los que se logran en la competencia simultánea simple. La extensión con la cual la firma algorítmica puede amenazar a la otra depende de la su habilidad para comprometerse: cuando el compromiso es bajo, la firma algorítmica tiene un incentivo de corto plazo para reducir sus precios dados los altos precios del rival. Por ejemplo, si la firma B fija un precio de 2, la firma A podría obtener mayores beneficios en el corto plazo si reduce su precio a 1,8 y capta la mayor parte de la demanda. Pero si A pudiera comprometerse a mantener un precio de 2, podría sostener ese equilibrio alto en períodos futuros, siempre que B no se desvíe.
Por último, los autores realizan un ejercicio en el que registraron los efectos sobre el bienestar del consumidor ante cada combinación entre α y γ. Como se puede observar en la Figura 4, las regiones están ordenadas de menor bienestar a mayor: la Región I corresponde a un bienestar del consumidor menor a aquel del equilibrio colusivo, la Región II indica un bienestar menor a aquel del equilibrio secuencial, y la Región III indica un bienestar menor al de la competencia simultánea. En este sentido, los autores señalan que tanto el bienestar del consumidor y el bienestar total pueden ser menores en un equilibrio coercitivo, en comparación con un equilibrio colusivo.
Figura 4: Bienestar del consumidor según la velocidad de reacción y el compromiso
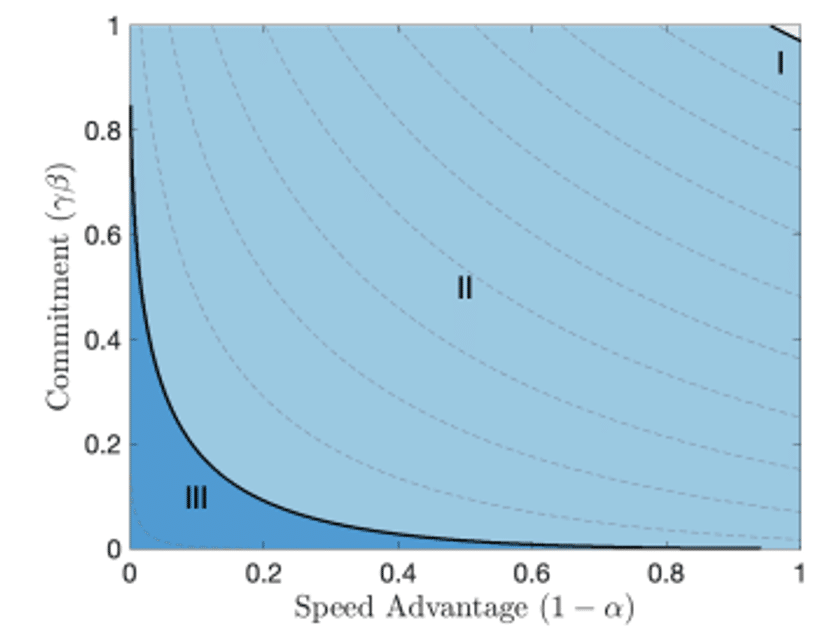
Extraído de Mackay y Brown, 2025, p. 18.
Este análisis pone en evidencia cómo dos características de los algoritmos —la velocidad y el compromiso— pueden dar lugar a precios más altos y otorgar una ventaja sustancial a la firma algorítmica, incluso cuando la firma rival está actuando en función de su propio interés de corto plazo. En este sentido, argumentan los autores, los resultados de este artículo revelan que, realmente, habría un espacio más amplio para que los algoritmos de precios eleven los precios, sin necesidad de acuerdos explícitos o implícitos entre competidores.
Por otro lado, los autores ligan estos resultados con el poder que tienen las plataformas digitales para manipular las mismas variables que estudian (velocidad para ajustar precios y el grado de compromiso). Exploran cómo diferentes funciones objetivo de estas —según si priorizan a productores, consumidores o una mezcla entre ellos— pueden afectar sus decisiones de adopción algorítmica (ver Nota CeCo: “Especial Concurrences Awards (2024): Algoritmos y diseño de plataformas digitales”).
En esta línea, concluyen que, si una plataforma tiene como objetivo maximizar el excedente del productor, entonces tiene incentivos a permitir que algunas firmas (que se encuentren dentro de la plataforma) adopten estos algoritmos con compromiso intertemporal y ventaja de velocidad. Así, la empresa suaviza la competencia sin necesidad de competencia directa entre los agentes rivales. Asimismo, los autores encuentran que cuando la plataforma asigna menor peso al bienestar del consumidor, elige combinaciones de parámetros más extremas en términos de ventajas de precios y compromiso, lo que favorece equilibrios con precios más altos.
De la misma forma, si la plataforma está integrada verticalmente —es decir, actúa como vendedora en su propio marketplace— y le interesaría priorizar las ventas de un solo vendedor, entonces el equilibrio implica darle la mayor ventaja de precios al vendedor integrado, en detrimento del resto de vendedores. Esta extensión del modelo ilustra cómo diferentes ponderaciones entre bienestar del productor y del consumidor pueden llevar a distintos valores endógenos para los parámetros de los algoritmos que manejan las plataformas.
Regístrate de forma gratuita para seguir leyendo este contenido
Contenido exclusivo para los usuarios registrados de CeCo