Cournot (modelo)

Supuestos del modelo

Supongamos un mercado compuesto por dos empresas competidoras (duopolio): empresa “i” y empresa “j”.

Además, consideramos los siguientes supuestos:

• En este mercado, los productos que se ofrecen son homogéneos. Esto significa que los consumidores no pueden distinguir de qué empresa proviene una unidad específica del bien. Por tanto, son perfectos sustitutos en términos de utilidad.
• Las empresas compiten ofreciendo cantidades del producto y toman sus decisiones de forma simultánea (es decir, la empresa “i” no conoce la cantidad que ofrecerá la empresa “j” al momento de decidir cuánta cantidad ofertar, y viceversa). En nomenclatura de teoría de juegos, se trata de un juego “simultáneo” o “estático” (en oposición a un juego “secuencial” o “dinámico”).
• Ambas empresas presentan la misma estructura de costos (costos simétricos), y no poseen restricciones de capacidad. Esto último quiere decir que las empresas no enfrentan restricciones que limiten su volumen de producción. Este supuesto se suele utilizar en la teoría económica para permitir que las empresas sirvan a todos los consumidores del mercado.
• Las empresas poseen información perfecta sobre la función de demanda del mercado y los costos de producción de sus rivales.

Interdependencia entre los competidores

Los modelos de competencia imperfecta se caracterizan por la interdependencia entre las acciones de los competidores, denominada interacción estratégica: cada empresa debe considerar lo que hará su rival al momento de tomar una decisión.

A continuación, demostramos que en el Modelo de Cournot existe una interacción estratégica entre las cantidades producidas por ambas empresas.

Sean “q_{i}” y “q_{j}” las cantidades del bien ofrecidas por las empresas “i” y “j”, respectivamente. La función de demanda “inversa”, P(Q), establece el máximo precio a pagar por los consumidores de un mercado (P), en función de la cantidad total ofrecida por los oferentes (Q). En otras palabras, mientras la función de demanda “convencional” muestra cómo la cantidad demandada por el consumidor varía según el precio, la función de demanda inversa muestra cómo el precio varía según la cantidad ofrecida. En ambos casos, la relación entre ambas variables es negativa: a medida que aumenta la cantidad ofrecida, el precio que los consumidores están dispuestos a pagar disminuye, y viceversa.

Dado que en este contexto solo existen dos empresas, la cantidad total ofrecida corresponde simplemente a la suma de las cantidades ofrecidas por ambas empresas, es decir: Q=q_{i}+q_{j}. Luego, la función de demanda inversa puede expresarse como P(q_{i}+q_{j}).

Por otro lado, la función de beneficio (o utilidad) de la empresa “i” es:

\pi_{i}=pq_{i}-C(q_{i})

Donde pq_{i} describe el precio (p) multiplicado por la cantidad ofrecida por la empresa “i” (q_{i}), representando así los ingresos totales de la empresa “i”; mientras que C(q_{i}) corresponde a la función de costos totales de la empresa “i” (la cual depende positivamente de la cantidad ofrecida por esta, es decir, a mayor cantidad ofrecido, mayor costo).

Reemplazando la función de demanda inversa en la función de beneficio (p=P(q_{i}+q_{j})), tenemos que:

\pi_{i}=P(q_{i}+q_{j})q_{i}-C(q_{i})

Es decir, los beneficios de la empresa “i” dependen de la cantidad ofrecida por la empresa “j”, pues esta afecta el precio de mercado a través de la función de demanda inversa (y la empresa “j” es consciente de ello). Esto es análogo para la empresa “j” (sus beneficios dependen de la cantidad ofrecida por la empresa “i”):

\pi_{j}=P(q_{i}+q_{j})q_{j}-C(q_{j})

Por ejemplo, una empresa podría reducir su producción con la intención de elevar el precio de mercado y aumentar sus beneficios. Sin embargo, si la otra empresa responde aumentando su producción, el efecto neto podría ser una disminución en los beneficios de la empresa que redujo su producción, dado que el precio no se mantendría lo suficientemente alto como para compensar su menor volumen de ventas.

En otras palabras, las estrategias de producción de ambas empresas están interconectadas, y cada una debe considerar la producción de la otra al tomar sus decisiones.

Equilibrio de Nash y funciones de reacción

Producto de esta interdependencia, para resolver el equilibrio competitivo de este modelo, se emplea el concepto de Equilibrio de Nash (“EN”), proveniente de la literatura de Teoría de Juegos. En un EN, cada jugador elige las estrategias que maximizan su beneficio esperado, considerando las acciones de los demás jugadores.

Dicho de otra manera, un EN es una combinación de estrategias en la que ningún jugador tiene incentivos para cambiar su estrategia unilateralmente, dado el conjunto de estrategias elegidas por los demás jugadores.

Un concepto clave en la obtención de un EN es lo que se conoce como “función de reacción” de una empresa, que caracteriza el comportamiento estratégico de las mismas. La función de reacción responde a la siguiente pregunta: ¿Cuál es la respuesta óptima de una empresa frente a la estrategia de su rival?

Como en este modelo las empresas compiten en cantidades, la función de reacción se define como la cantidad a ofrecer óptima de una empresa, dada la cantidad ofrecida por su competidor. En particular, en el caso de la empresa “i”, su función de reacción se denota como q_{i}^{\ast}(q_{j}); es decir, la cantidad q_{i}^{\ast} que maximiza las ganancias percibidas por la empresa “i”, ante una determinada cantidad ofrecida por su rival (q_{j}).

De esta forma, podemos obtener la función de reacción de la firma “i” maximizando su función de beneficio, considerando como dada (es decir, como si fuera una constante) la cantidad ofrecida por la empresa “j” (q_{j}).

Siguiendo a Church & Ware (2000), asumiremos las siguientes formas funcionales para simplificar la resolución analítica del problema:

-Función de demanda inversa lineal:

P(Q)=A-bQ=A-b(q_{i}+q_{j})

Donde A y b son parámetros positivos que representan el intercepto y la pendiente de la función, respectivamente.

-Costos marginales constantes y ausencia de costos fijos:

C(q_{i})=cq_{i}, C(q_{j})=cq_{j}

Así, la función de costos totales se compone únicamente por costos variables (cantidad multiplicada por costo marginal), donde c corresponde al costo marginal (positivo e idéntico para ambas empresas).

El costo marginal se define como el cambio en el costo total que resulta de la producción de una unidad adicional. Matemáticamente, este se calcula como la derivada de la función de costos totales, C(q):

C'(q)=c.

Considerando estas expresiones, la función de beneficio de la empresa “i” es:

\pi_{i}=[A-b(q_{i}+q_{j})]q_{i}-c(q_{i})

En economía, el procedimiento estándar para optimizar una función objetivo —en este caso, maximizar la función de beneficio de la empresa “i”— es derivar en función de la variable de decisión —en este caso, la cantidad ofrecida por la empresa “i” (q_{i})—.

Derivar la función de beneficio con respecto a q_i nos dice cómo cambia el beneficio de la empresa “i” cuando esta decide producir una unidad adicional de producto. La condición de primer orden es una regla que indica que la cantidad óptima —aquella que maximiza el beneficio de la empresa “i”— se encuentra en el punto en que la derivada de la función de beneficio es igual a 0. La intuición es que si la empresa “i” decide producir una unidad más o una menos desde este punto, su beneficio empezará a disminuir.

Así, derivando en función de q_{i} (considerando q_{j} como dado), la condición de primer orden es:

A-2bq_{i}-bq_{j}-c=0

Reordenando para despejar q_i, la función de reacción de la empresa “i” es:

q_{i}^{\ast}(q_{j})=\frac{A-c-bq_{j}}{2b}

Debido a que los costos marginales son simétricos, la expresión para la función de reacción de la empresa “j” es análoga:

q_{j}^{\ast}(q_{i})=\frac{A-c-bq_{i}}{2b}

Gráficamente, las funciones de reacción asumen la siguiente forma:

Gráfico N°1: Funciones de reacción con costos simétricos

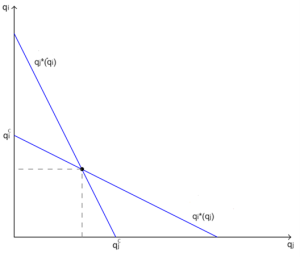
Fuente: Adaptado de Llaupi (2021)

Como se aprecia en el Gráfico N°1, la función de reacción de cada empresa decrece en la medida que aumenta la cantidad ofrecida por la otra empresa. A esta relación negativa entre las variables de competencia se les denomina sustitutos estratégicos: mientras más produzca la firma “j”, menor será la cantidad que le convendrá producir a la firma “i” (González, 2020).

Dado que q_{i}^{\ast} y q_{j}^{\ast} representan la mejor respuesta de la empresa “i” y “j” ante la cantidad ofrecida por su rival, es posible cerrar el modelo reemplazando una función de reacción dentro de la otra. Gráficamente, este ejercicio consiste en encontrar la intersección entre ambas funciones de reacción.

Reemplazando q_j* dentro de q_i*, se obtiene:

q_{i}=q_{i}^{\ast}(q_{j})=\frac{A-c-b(\frac{A-c-bq_{i}}{2b})}{2b}

Reordenando para despejar q_i, llegamos a que:

q_{i}^{C}=\frac{A-c}{3b}

De forma análoga, reemplazando esta cantidad en la función de reacción de la empresa j:

q_{j}^{C}=\frac{A-c}{3b}

Donde q_i^C y q_j^C corresponden a las cantidades de equilibrio obtenidas en el Modelo de Competencia de Cournot. Como es de esperar, ambas cantidades son idénticas, pues las funciones de costo de ambas empresas son simétricas y ambas deciden la cantidad a ofertar al mismo tiempo.

A su vez, la cantidad total ofrecida es:

Q^{C}=q_{i}^{C}+q_{j}^{C}=\frac{2(A-c)}{3b}

Para obtener el precio, reemplazamos la cantidad total (Q^C) en la función de demanda inversa:

P^{C}=P(Q^{C})=\frac{A+2c}{3}

De esta forma, el precio de equilibrio es superior al costo marginal. Por lo tanto, en el Modelo Base, las empresas ejercen —en equilibrio— poder de mercado (precisamente por tener la capacidad de cobrar un precio superior al costo marginal).

Por lo tanto, los beneficios obtenidos por cada empresa son positivos:

\pi_{i}^{C}=\pi_{j}^{C}=\frac{{(\frac{A-c}{3})}^2}{b}

A modo de referencia, se pueden comparar estas cantidades y precios de equilibrio con los resultados que se obtendrían en escenarios de competencia perfecta y monopolio (suponiendo las mismas formas funcionales para la demanda y los costos de las empresas).

En competencia perfecta, la cantidad total producida y el precio de equilibrio son:

Q^{CP}=\frac{A-c}{b}, P^{CP}=c

En un contexto monopólico, estas variables son:

Q^{M}=\frac{A-c}{2b}, P^{M}=\frac{A+c}{2}

De esta manera, la Competencia de Cournot se sitúa como un punto intermedio entre los equilibrios de competencia perfecta y monopolio:

Q^{M}<Q^{C}<Q^{CP},

P^{CP}<P^{C}<P^{M}

La cantidad total producida en el Modelo de Cournot es inferior a la que se observaría en un mercado de competencia perfecta, pero supera a la que generaría un monopolio. Asimismo, el precio de equilibrio en este modelo excede los costos marginales, a diferencia de lo que ocurriría en un escenario de competencia perfecta, donde el precio se equipara al costo marginal. No obstante, el poder de mercado ejercido por las empresas no es tan grande como el que detentaría un monopolio.

Supuestos del modelo

El Modelo Base puede extenderse para considerar un número mayor —pero finito— de empresas.

Así, en lugar de suponer que existen dos competidores, ahora asumiremos que el mercado está compuesto por N empresas competidoras. Por otro lado, seguiremos suponiendo: (i) bienes homogéneos; (ii) costos simétricos; (iii) simultaneidad de las decisiones; e (iv) información perfecta

Equilibrio de Nash y funciones de reacción

En este contexto, la cantidad total ofrecida (Q) corresponde a la suma de las cantidades individuales ofrecidas por las N empresas presentes en el mercado:

Q=q_{1}+q_{2}+...+q_{N}=\sum_{i=1}^{N}q_{i}

Utilizaremos la expresión \sum_{i=1}^{N}q_{-i} para referirnos a la suma de las cantidades ofrecidas por todas las empresas presentes en el mercado, a excepción de la empresa “i”. Luego, asumiendo las mismas formas funcionales que en la sección anterior, la función de beneficio de la empresa “i” es:

\pi_{i}=A-b(q_{i}+\sum_{i=1}^{N}q_{-i})q_{i}-cq_{i}

Derivando en función de q_i (considerando \sum_{i=1}^{N}q_{-i} como dado), la condición de primer orden de la empresa “i” es:

A-2bq_{i}-b\sum_{i=1}^{N}q_{-i}-c=0

Reordenando para despejar q_{i}, la función de reacción de la empresa “i” es:

q_{i}^{\ast}(\sum_{i=1}^{N}q_{-i})=\frac{A-c-b\sum_{i=1}^{N}q_{-i}}{2b}

Debido a que los costos marginales son simétricos, las funciones de reacción de las demás firmas tienen la misma forma funcional.

En este escenario, el EN es representado por un vector q^{\ast}=(q_{1}^{\ast},q_{2}^{\ast},...q_{N}^{\ast}) —esto es, un elemento matemático que agrupa las cantidades individuales de todos los competidores—, tal que para toda empresa “i” se cumpla que:

q_{i}^{\ast}(\sum_{i=1}^{N}q_{-i})=\frac{A-c-b\sum_{i=1}^{N}q_{-i}^{\ast}}{2b}

Es decir, consiste en un equilibrio donde todas las empresas están jugando sus mejores respuestas simultáneamente, y nadie tiene incentivos unilaterales para desviarse de su estrategia actual.

Producto de la simetría de costos, las cantidades ofrecidas por cada empresa serán idénticas en equilibrio —como verificamos que ocurría en el caso de un duopolio—. Esto nos permite establecer que:

q_{1}^{\ast}=q_{2}^{\ast}=...=q_{N}^{\ast}

Entonces:

\sum_{i=1}^{N}q_{-i}^{\ast}=(N-1)q_{i}^{\ast}

Reemplazando en la función de reacción de la empresa “i”:

q_{i}^{\ast}(\sum_{i=1}^{N}q_{-i})=\frac{A-c-b(N-1)q_{i}^{\ast}}{2b}

Reordenando para despejar q_i^*:

q_{i}^{C}=q_{i}^{\ast}= \frac{A-c}{(N+1)b}

Donde q_{i}^{C} corresponde a la cantidad de equilibrio obtenida por la empresa “i” (la cual es idéntica para las N empresas presentes en el mercado).

En consecuencia, la cantidad total ofrecida es:

Q^{C}=Nq_{i}^{C}=\frac{N(A-c)}{(N+1)b}

Reemplazando en la función de demanda inversa, el precio de equilibrio es:

P^{C}=P(Q^{C})=\frac{A+Nc}{N+1}

Así, en principio, las empresas ejercen poder de mercado (pues el precio es mayor al costo marginal).

Similarmente, se puede verificar que los beneficios de las empresas son positivos en equilibrio:

\pi_{i}^{C}=\frac{{(\frac{A-c}{N+1})}^2}{b}

En la medida que aumenta el número de empresas presente en el mercado (N), los resultados de este modelo (precio, cantidades y beneficios) se acercan cada vez más a los resultados de competencia perfecta. En efecto, el precio y los beneficios de las empresas son decrecientes respecto al número de competidores (N), mientras que la cantidad ofertada (Q) es creciente respecto a esta variable.

En el extremo, se puede verificar que, cuando el número de competidores tiende a infinito (\lim_{N\to\infty}), el precio de equilibrio de Cournot se iguala al costo marginal; los beneficios se reducen a cero; y la cantidad ofertada se equipara a la que se produciría en un mercado perfectamente competitivo (replicándose así el resultado de competencia perfecta).

P^{C}=\lim_{N\to\infty} \frac{A+Nc}{N+1}=c
\pi_{i}^{C}= \lim_{N\to\infty} \frac{{(\frac{A-c}{N+1})}^2}{b}=0
Q^{C}=\lim_{N\to\infty}\frac{N(A-c)}{(N+1)b}=\frac{A-c}{b}

Siguiendo a Church & Ware (2000), consideramos un mercado con dos empresas (“i” y “j”), que compiten en cantidades. A diferencia del Modelo Base de Cournot, esta variante considera que las empresas tienen costos de producción diferentes (“costos asimétricos”).

En particular, sus funciones de costos son:

C(q_{i})=c_{i}q_{i}, C(q_{j})=c_{j}q_{j}

Donde se cumple que c_{j}<c_{i}, es decir, la empresa “j” es más eficiente que la empresa “i” para cualquier cantidad positiva de producción (pues tiene menores costos de producción). Por lo tanto, sus funciones de beneficio difieren (nuevamente suponemos una función de demanda inversa lineal):

\pi_{i}=[A-b(q_{i}+q_{j})]q_{i}-c_{i}q_{i}, \pi_{j}=[A-b(q_{i}+q_{j})]q_{j}-c_{j}q_{j}

Derivando en función de q_{i} (considerando q_{j} como dado), la condición de primer orden de la empresa “i” es:

A-2bq_{i}-bq_{j}-c_{i}=0

Reordenando para despejar q_{i}, la función de reacción de la empresa “i” es:

q_{i}^{\ast}(q_{j})=\frac{A-c_{i}-bq_{j}}{2b}

Siguiendo el mismo procedimiento, se puede verificar que la función de reacción de la empresa “j” es:

q_{j}^{\ast}(q_{i})=\frac{A-c_{j}-bq_{i}}{2b}

De esta manera, las funciones de reacción de ambas firmas ya no son equivalentes, como ocurría en el caso con costos simétricos. Esto se observa en el Gráfico N°2:

Gráfico N°2: Funciones de reacción con costos asimétricos

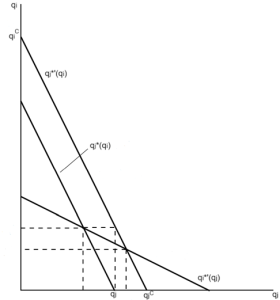
Fuente: Adaptado de Church & Ware (2000)

Como ilustra esta figura, la función de reacción con costos simétricos corresponde a la recta q_{j}^{\ast}. Luego, un menor costo marginal significa un desplazamiento de la función de reacción de la empresa “j” hacia afuera (representado por la recta q_{j}^{\ast}‘). Esto indica que, para cada cantidad producida por la empresa rival, la empresa con menores costos (en este ejemplo, la empresa “j”) está dispuesta a producir más que en la situación donde tenía los mismos costos que su rival.

Realizando nuevamente el ejercicio de introducir una función de reacción dentro de la otra (para así encontrar el EN), obtenemos las siguientes cantidades de equilibrio:

q_{i}^{C}=\frac{A-2c_{i}+c_{j}}{3b},

q_{j}^{C}=\frac{A-2c_{j}+c_{i}}{3b}

Luego, la cantidad producida por una empresa depende negativamente del costo propio, y positivamente del costo del rival. En consecuencia, la empresa “j” (más eficiente) producirá una mayor cantidad de producto que la empresa “i”. Mientras mayor sea la asimetría de costos, mayor será la asimetría entre las cantidades producidas por ambas empresas.

En esta línea, la empresa con menores costos producirá una mayor cantidad de producto que la cantidad que ofrecería en un escenario con costos simétricos (lo contrario sucede para la empresa con mayores costos; es decir, producirá menos que en un escenario de costos equivalentes).

El Modelo de Stackelberg (también conocido como “Competencia de Stackelberg”, “Competencia Líder-Seguidor” o “Modelo de Liderazgo”) supone un escenario en que las empresas deciden sus cantidades de producción de forma secuencial, en lugar de simultánea.

En concreto, pensamos en un mercado conformado por dos empresas simétricas, “i” y “j”, que compiten en cantidades. Siguiendo a Church & Ware (2000), este juego secuencial contempla dos periodos:

– Primer periodo (t=1): la empresa “i” decide la cantidad q_i que ofrecerá en el mercado.

– Segundo periodo (t=2): la empresa “j”, luego de observar la decisión de la empresa “i” (q_{i}), decide producir la cantidad q_{j}.

Dado que la empresa “i” decide su cantidad antes que la empresa “j”, en el contexto de este modelo, las empresas “i” y “j” son referidas como “líder” y “seguidora”, respectivamente.

Por un lado, la función de reacción de la empresa “j” es la misma que en el Modelo Base (suponiendo las mismas formas funcionales que en dicha sección):

q_{j}^{\ast}(q_{i})=\frac{A-c-bq_{i}}{2b}

Ahora bien, debido a que la empresa “i” posee información perfecta sobre la función de reacción de la firma “j”, la empresa “i” puede anticiparse a la respuesta óptima de la empresa “j”. En concreto, la empresa “i” sabe que, si decide producir q_{i} en el primer periodo, la empresa “j” responderá ofreciendo q_{j}^{\ast}(q_{i}) en el segundo periodo.

Matemáticamente, esto equivale a que la empresa “i” introduzca la función de reacción de la empresa “j” dentro de su función de beneficio. Considerando las mismas formas funcionales que en las secciones anteriores, tenemos que:

\pi_{i}=[A-b(q_{i}+q_{j}^{\ast}(q_{i}))]q_{i}-cq_{i}

\pi_{i}=[A-b(q_{i}+\frac{A-c-bq_{i}}{2b})]q_{i}-cq_{i}

Luego, la firma “i” simplemente maximiza esta función para decidir cuánta cantidad producir. Así, derivando en función de q_{i}, la condición de primer orden es:

\frac{A}{2}-\frac{c}{2}-bq_{i}=0

Reordenando para despejar q_{i}, la cantidad de equilibrio para la empresa “i” en el Modelo de Stackelberg es:

q_{i}^{S}=\frac{A-c}{2b}

Reemplazando en la función de reacción de la empresa j, la cantidad de equilibrio para esta empresa es:

q_{j}^{S}=\frac{A-c}{4b}

De esta forma, se observa que:

q_{i}^{S}>q_{i}^{C}

q_{j}^{S}<q_{j}^{C}

Respecto al Modelo Base (elaborado para un juego estático), la empresa que decide primero —en este caso, la empresa “i” o “líder” —, produce una mayor cantidad de producto en la Competencia de Stackelberg (juego secuencial). Por el contrario, la empresa seguidora produce una menor de cantidad de producto en este nuevo escenario.

Así, la intuición detrás del Modelo de Stackelberg es que la empresa líder intentará “copar” o “saturar” el mercado, dejando con menor espacio a su competidora, que se verá presionada a reducir su producción para no deprimir demasiado el precio.

El 30 de noviembre de 2011, la FNE requirió a tres empresas productoras de pollo (Agrosuper, Ariztia y Don Pollo), y a la Asociación de Productores de Pollo (APA), ante el TDLC. Estas entidades fueron acusadas de celebrar un acuerdo colusorio que limitaba la producción de pollo, controlando la cantidad producida y ofertada en el mercado nacional.

El TDLC acogió el requerimiento y multó a las tres empresas y a la APA por colusión, lo cual fue confirmado por la Corte Suprema. Para determinar el monto de las sanciones económicas impuestas, el TDLC consideró, entre otros factores, el beneficio económico obtenido por las empresas a raíz del acuerdo anticompetitivo.

Al respecto, la FNE presentó un informe económico titulado “Estimación de los daños económicos generados por la colusión en la industria de pollo en Chile”, elaborado por los economistas Andrés Gómez-Lobo y José Luis Lima. El objetivo de este informe fue estimar los precios que se habrían observado en un escenario competitivo —es decir, si los productores de pollo no hubiesen incurrido en el acuerdo colusorio—, para así determinar el beneficio obtenido por las empresas como consecuencia del cobro de un mayor precio durante el periodo analizado.

Para realizar esta estimación, los autores supusieron una estructura competitiva bajo el Modelo de Stackelberg (pág. 26). Como vimos, este modelo considera un mercado donde las empresas compiten en cantidades de forma secuencial, siguiendo una lógica de líder-seguidor: las empresas líderes fijan su cantidad de producción tomando en cuenta la reacción que genera su oferta en los seguidores, quienes simplemente se acomodan a la demanda residual.

En este caso, según la argumentación de los autores, las empresas sancionadas —Agrosuper, Ariztía y Don Pollo—, que representaban el 80% de las ventas del mercado, operaban como líderes, mientras que las empresas remanentes —Santa Rosa, Codipra e importadoras— funcionaban como seguidoras.

Tomando este modelo como referencia, los autores estimaron que la colusión generó daños del orden de 33,3 millones de UF (pág. 30) (equivalente a 1.263 millones de dólares, al tipo de cambio de abril 2024).

El 28 de diciembre de 2017, el TDLC sancionó a las empresas CMPC Tissue S.A (“CMPC”) y SCA Chile S.A (“SCA”) por colusión de precios y cuotas de mercado en productos de papel tissue, entre los años 2000 y 2011.

Con fecha 6 de abril de 2020, Papelera Cerrillos S.A (“Papelera Cerrillos”) presentó una demanda de indemnización de perjuicios en contra de CMPC y SCA ante el TDLC, con motivo de los daños que habría sufrido por los actos ilícitos sancionados. De acuerdo a la demandante, las acciones de los demandados tuvieron como efecto la supresión de la competencia y, en última instancia, su fracaso financiero.

Sin embargo, el TDLC rechazó la demanda, afirmando que las pérdidas económicas de Papelera Cerrillos tenían una explicación multicausal, ajena a la conducta sancionada. Para justificar su decisión, el TDLC citó los resultados del informe económico “Informe económico sobre la demanda de Papelera Cerrillos S.A.”, elaborado por Fernando Luco a petición de CMPC.

El informe rechazó la racionalidad económica de los argumentos presentados por Papelera Cerrillos, argumentando que la existencia de un cartel debería aumentar las utilidades de un competidor independiente, en lugar de reducirlas como argumentaba la demandante. Para esto, el autor se basó en las implicancias de la Competencia de Cournot y otros modelos oligopólicos.

En efecto, el informe demuestra que, según los fundamentos del Modelo de Cournot para un mercado compuesto por tres empresas, donde dos de estas forman un acuerdo colusorio, las utilidades de la tercera firma son mayores en presencia de un cartel que en el equilibrio competitivo, para un rango amplio de parámetros (pág. 13).